How to get the ChiSq for each predictor in Logistic Regression?

[#1]

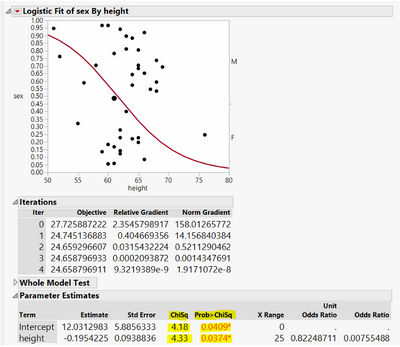
I noticed that in Logistic Regression each predictor will have a ChiSq value as highlighted in the color yellow below pic, I am wondering how to calculate this value for each predictor since the predictors are continuous data.

Is there anyone who can help answer? Thanks in advance. ~ ~

[#2]

It is just the square of the (estimate / standard Error)².  You can find this in the JMP help files.

[#3]

Thanks for your answer.

But what I want to ask more is that what the physical meaning of prob is? I mean what does this ChiSq compare to? As above the Prob of Height = 0.0374 is less than 0.05, so what does this tell us? Does this mean that the value of parameter Height cannot be 0 or must be considered in the model? 

[#4]

@ih answered your original question on calculating the statistic.

The following tries to answer your follow-up questions.

You pretty much understand what it does. "ChiSquare" and "Prob>ChiSq" tells the result of comparing the estimate with zero. Here the probability 0.0409. It is calculated as the probably that a Chi-Sqaure random variable with 1 degree of freedom is larger than the test statistic 4.18. Loosely speaking, it says that if everything goes well (e.g. model is correct), and if you conclude that intercept is significant, you could be wrong with a small probability 0.0409 (Type I error).

Please check out literature on hypothesis testing, Type I and Type II errors. Read linear regression would be a good start.

In linear regression, we use "t-Ratio". According to linear model theory, the "t-Ratio" statistic should follow a Student-t distribution. So if the "t-Ratio" statistic is too small (negative to the left) or too big "positive to the right", it implies that one would less likely be wrong if one concludes that the parameter is significant.

Here in logistic regression, we don't have a "t-Ratio" statistic. The theory gives us "ChiSquare". And an extreme "ChiSquare" (extreme to the right) statistic implies that one would less likely be wrong if one concludes that the parameter is significant.