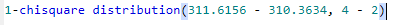How to customize Loglikelihood Contour plots of 2 Weibull models?

[#1]

Hello,

I am working on comparing two Weibulls models, to check if they are significantly different.

Based on "The Weibull Handbook" by R.Abernethy chapter 7.5.3 I would like to compare Likelihood Contour Plots of two models.

I use a Life Distribution - Compare Group panel to conduct the analysis. It creates a two separate Parametric Estimates - Weibull models. From there I can select to "Show Likelihood Contour".

To begin with, I would like to ask if there is a possibility to customize those charts, like reduce the number of levels, or change the contour colors?

I know that later I can combine the contours for two models using "Copy Frame Contents".

Moreover, is there a way to extract the actual points that create the contour? In the end I would like to check automatically if the models' contours intersect or no, and for that purpose I think that I must be  using actual points.

Thank you for your help.

Regards,

Ceg1

[#2]

The functions of customizing and extracting points from contour are not available. The purpose of that section in the handbook is to visually compare the fits. It is great that you mentioned that you know how to make a similar plot using JMP. However, the plot is not an replacement of or alternative to a formal test. On the same subject and related discussions, you may be interested in section 12.3 in "Statistical Methods for Reliability Data", 2nd. ed. by Meeker et.al. To performance a likelihood ratio test on whether the Weibull fits of the two groups are significantly different or not, you may want to investigate how to use Fit Life by X platform. Here is an example of how you should configure the launch dialog

Choose "Weibull", if that is desired. If your grouping variable is discrete, you have nothing else to worry about. If not, make sure choose "No Effect", "Location" or "Location Scale" in the Relationship combo box. Each of the three represents a hypothesis, loosely speaking: "Two groups are same", "Two groups are different by Location, or Scale parameter Alpha for Weibull", "Two groups are different by both parameters". The platform provides a comprehensive analysis for you to compare them.

[#3]

Thank you for your answer. I was not aware of this functionality. I gave it a try and I am not convinced that this platform helps me to answer my question. 

I am not sure how should I interpret the results of Nested Test. I have a discrete, character, grouping variable. Fit Life platform returns such Test Results. 

What I understand from JMP manual is that if "Prob>ChiSq" is less that significance level (usually 0.05), then we can reject the null hypothesis that those two models are different significantly one from another.

However, there are 2 tests, whereas I think that I would like to test the hypothesis between No Effect vs. Location and Scale. Can you explain to me how those test results should be interpreted, as I think I am missing some information?

Thank you.

[#4 · Accepted solution]

Your thinking process is exactly right. And you won't find the explicit result for the test "No Effect vs. Location and Scale", which states the null hypothesis that scale and shape parameters are the same.

That test, by itself, is insufficient to give additional insight if the null is rejected. And additional tests are needed. In that case, it will end up with a nested test. Let me use this example to explain why nested test is useful for decision making.

In this example with two groups, one is usually interested in whether their reliabilities are same, or one is more reliable than the other, so one can take proper actions accordingly. When both tests come back insignificant (denote this Scenario 1), then one can conclude that their reliabilities are not different, then take an action. If "No Effect vs Location" is significant, but "Location vs Location and Scale" is insignificant (denote this Scenario 2), one can conclude that one is more reliable than another other in the conventional sense, then take an action. In the remaining two scenarios (denote them Scenario 3 and 4), one can only conclude that the two groups are different, but cannot draw conclusion on whether one group is definitely more reliable. A further analysis is required, or the criteria of being more reliable needs additional specifications, e.g. defined by comparing B10 life.

So what about the "No Effect vs Location and Scale", which is not there. But think about it, if it cannot be rejected, it means Scenario 1; if it is rejected, it means one of the other three scenarios, but cannot tell which. So the nested test can directly lead to decision making about the most common interests, but "No Effect vs Location and Scale" cannot.

P.S. though I describe the decision making process as a multiple testing, it is often like a sequential test in practice. I.e. it seems rare if "No Effect vs. Location" is insignificant but "Location vs Location and Scale" is significant. So one may describe two groups are no difference just based on the first test without further elaboration. Also if you do want the test result for "No Effect vs Location and Scale", it Likelihood Ratio Test statistic is 311.6156 - 310.3634 = 1.25219999999996, the difference of -2Loglikelihood from the two models. And the critical value is 1-alpha quantile of Chi-Sqaure with df = 4-2, the difference of the Number of Parameters from the two models. The p-value is 0.534672964662089, using the following calculation:

Ref: https://en.wikipedia.org/wiki/Likelihood-ratio_test

[#5]

Hi, thank you for your reply.

In fact, I incorporated the Fit Life by X platform to my script to compare two Weibull models and I use Nested Tests as well.

However, I played little bit with the tool and I have a question. 

From what I understood, "No Effect" stage creates a 2-parameter Weibull model based on both merged samples. 

Can you tell me, how does JMP handles such cases, when there is only minor change between population?

For example, I have model based on 5 failures and 10 suspensions, and I want to compare it with new model, that is based on the same data, but there is one additional failure. (so 6 failures and 10 suspensions in total). Time censoring values does not change between the models.

So for me it seems that the merged model would be built on two sets of almost identical points and it seems incorrect to me. 

Additionally, can you guide me to any paper/book/article, where the Nested Tests for reliability applications are described in greater detail?

Thank you,

Regards,

Ceg1

[#6]

I am not sure that I understand the new scenario. Here is my understanding. You have a data in which there are 5 failures and 10 suspensions. Then you add another failure to the data, and the data set now has 16 observations. Then you treat two data sets as two groups and go through Fit Life by X to "compare" the two groups. It does not feel right to me either. But may not mean the analysis has not meaning at all. It think it is down to the objective, what is the question of interest?

This sounds like what you are interested in: now there is a new observation, does my conclusion still hold on the previous 15 observation? If that is the case, here are some thought and additional questions:

1. It this observation is a lone star by itself, and no other information, I don't see other ways, and I don't see what can be worse by doing it.
2. If this observation is part of on-going additional test, this may fall into different types of analysis. One is to assess the model on the new data (does the failure rate agree with what the model predicted). Another that I can think of is to demonstrate your new data has the desired reliability (look for Reliability Demonstration", for which you need prior information about the reliability, which could be from your previous data). You might be interested in Chapter 14 Planning Reliability Demonstration Tests and 15 Prediction of Failure Times and the Number of Future Field Failures in this book: Statistical Methods for Reliability Data. 2nd. ed. 

For the nested tests, it is a regular hypothesis testing technique known as Likelihood Ratio Test. Here is a link to the wiki page: Likelihood-ratio test The first sentence on the page summarizes the technique very well. But you may try out different resources until find one which is suitable. Statistics textbooks should be a good direction to look at. The appendix of the above book that I mentioned also briefly explains the topic.