- JMP will suspend normal business operations for our Winter Holiday beginning on Wednesday, Dec. 24, 2025, at 5:00 p.m. ET (2:00 p.m. ET for JMP Accounts Receivable).
Regular business hours will resume at 9:00 a.m. EST on Friday, Jan. 2, 2026. - We’re retiring the File Exchange at the end of this year. The JMP Marketplace is now your destination for add-ins and extensions.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- How to conduct a binomial distribution analysis in JMP 14.1.0
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
How to conduct a binomial distribution analysis in JMP 14.1.0
Hello,
Could someone help with this query (attached an example dataset)
I'd like to do a binomial dist. analysis (in JMP) on mortality data count by treatment (4 treatments) and day (3-time points).
thanks
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to conduct a binomial distribution analysis in JMP 14.1.0
- Import data into JMP.
- Describe your data, or how you collected the data. Describe variables and observations. Clean your data if necessary. There are 4 time points, and observations at time=0 are inconsistent with others, I believe.
- If you have decided the objective of fitting Binomial, then ask the question: what is the number of trials, and the number of either death or survival. I believe you also have to ask "at what time point".
- Be careful, if you want to throw the data without modification into Logistic regression or similar analysis, because I believe that your observations, as is, are not independent. Need to see your description to confirm.
- If the objective is to model mortality rate over time, then Binomial may not be a relevant subject. Mortality rate over time is a curve.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to conduct a binomial distribution analysis in JMP 14.1.0
thank you Liu
The objective of the analysis is to see if the treatment (4 levels) has an effect on mortality and if the treatment effect changes over time.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to conduct a binomial distribution analysis in JMP 14.1.0
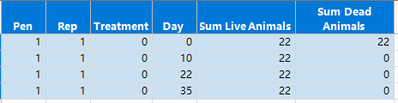
You data have 64 unique pens. Sum Live Animals are all 22 or less. But Sum Live Animals are all 22 on Day=0. Sum Live Animals will only decrease over time for individual pens. My questions: do all your pens start with 22 live animals on day=0, then over time, some animals will die, and are you tracking live and dead animals in individual pens?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to conduct a binomial distribution analysis in JMP 14.1.0
That's right. At the start of the study (day 0), all the 64 pens start with 20 animals in each pen.
The number of dead animals at each time point (day 0, 10, 22, 35) is recorded in column 6 (Sheet1).
There are 4 treatments, each treatment is replicated 16 times.
The treatment effect overtime on the number of dead animals is the variable of interest.
The data is presented (Sheet1) as:
- column 1: Pen ID
- column 2: Replicate
- column 3: Treatment ID
- column 4: Time point
- column 5: Number of alive animals
- column 6: Number of dead animals
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to conduct a binomial distribution analysis in JMP 14.1.0
The description clarifies a lot now. And it confirms that your observations as you tabulated are not independent. Look at the extreme case for Pen=1. Assuming the Sum Dead Animals at Day=0 is an error, and should have been 0. The four observations are recording the responses from the same group of 22 animals.
Despite the problem can be handled differently, this type of studies are the subject of survival analysis. Following are some simplest questions of interest in your study.
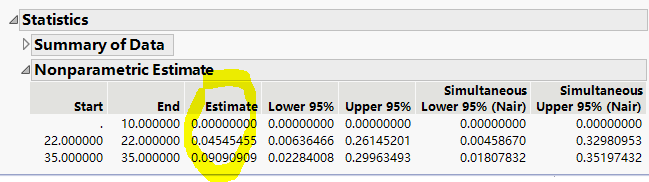
- What is the survival rate in Pen = 1, through Day = 22? The answer is 100%. And the complement death rate is 0%.
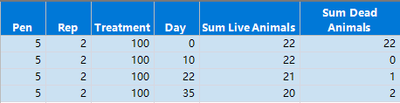
- What is the survival rate in Pen = 5, through Day = 22? The answer is 21/22=95.5%, because one animal died between Day = 10 and Day = 22, assuming no animals are died precisely on Day = 0, 10, 22, or 35. The complement death rate is 4.5%.
- What is the survival rate in Pen = 5, through Day = 35? The answer is 20/22=90.9%,because another animal died between Day = 22 and Day = 35. The complement death rate is 9.1%.
This is the screenshot of Pen = 5 data.
In your study, what variable has a Binomial distribution? This is: the number of death (or survival) in a Pen within a given time interval.
The death rate over time in a Pen is also a distribution. But this is not a Binomial. This is the reason for the way that I commented earlier.
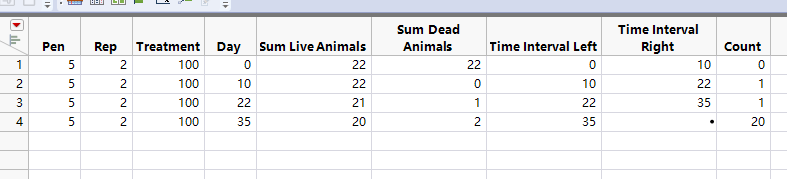
Now I explain how to conduct simple survival analysis like what I did above on this data. First you need to transform your data to a different format. Following is the transformed data for Pen = 5.
Step 1, I create two columns: "Time Interval Left" and "Time Interval Right", and enter values as in the following screenshot. This should be same for all pens. The first row of the two columns define a time interval from Day = 0 to Day = 10. The second and third rows define subsequent time intervals similarly. The last row define the time horizon after Day = 35.
Step 2, I create "Count" and put values as in the screenshot for Pen = 5. The values should be based on the death and survival counts in individual pens. For Pen = 5, the meanings are: there where no death in the 1st time interval; there is one death in the second time interval; there is one death in the third time interval; all remaining 20 survived at the time point Day = 35.
For more detailed explanation of this format, see the documentation for Life Distribution platform https://www.jmp.com/support/help/en/15.2/index.shtml#page/jmp/event-plot.shtml#
Notice, I only create a table for Pen = 5. And the following illustration is on that Pen only.
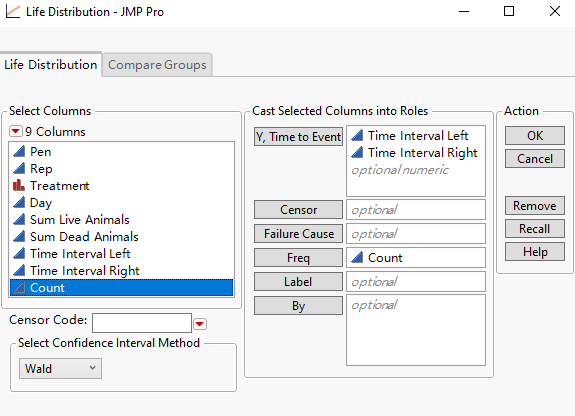
Next, go to Analyze menu, find "Reliability and Survival", the "Life Distribution", and specify the launch dialog like the following, then click "OK".
The default report shows results for "death rate". You may go to the red triangle menu in the report and find "Show Survival Curve" toggle between "death rate" and "survival rate" results.
Near the bottom of the report is the "Nonparametric Estimate" outline node, open it. It has the death rate estimates that I mentioned previously.
The above is just for one pen. You may be able to follow this path and go a long way after collecting the death (survival) rates for all pens at those time intervals. You can compare them by pen, treatment, etc.
If you convert all your data as I illustrated, you may also conduct more comprehensive analysis to estimate death rates with grouping variables simultaneously. If you can follow up with the converted data, I may have additional suggestions, depending what I can find in your data.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to conduct a binomial distribution analysis in JMP 14.1.0
Indeed the data was not properly described in the column headings (original file). The columns had data on live animals.
I've now attached the data on mortality instead.
I will look into the survival test you have proposed.
Thank you for the detailed explanation.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to conduct a binomial distribution analysis in JMP 14.1.0
Hello,
I have followed your proposal for survival analysis.
In the attached excel, you will find the data transformed (for all pens), which I believe follows what you've illustrated for pen 5 (columns for 'Time Int Left' & 'Time Int Right' and 'Count').
Then I conducted the survival analysis, life distribution analysis by Treatment (stats output attached).
Is this what you were proposing?
I'm not familiar with the survival output so would need some guidance on the meaning.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to conduct a binomial distribution analysis in JMP 14.1.0
Another potentially useful analysis in this case is probit analysis. You might postulate these effects using Analyze > Fit Model:
You can use the GLM platform to explore signficant effects, lack of fit, over-dispersion, and profile the response, Prob( Dead ).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to conduct a binomial distribution analysis in JMP 14.1.0
thank you.
That's what I was looking for but wasn't sure about the function logit or probit.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us