How to analyze binary outcomes time course data with multiple effects including interactions?

[#1]

Hi JMP Community,

I routinely analyze binary outcomes such as Response / Non-Response at a single time point in my research using the Nominal Logistic Platform. Now, I need to expand my analysis to incorporate the factor of Time in my model, and I realized that I am unsure about the best approach to do so. 

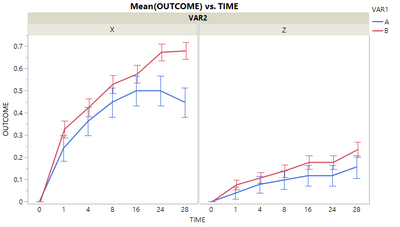
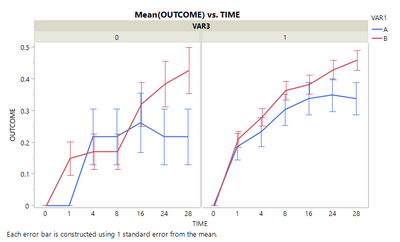
Specifically, in the mock data file attached to this post, I need to evaluate the effect of Time, VAR1, and VAR1 * Time for each level of VAR2 and VAR3 (see plot below), considering possible interactions between VAR1 and VAR2, and VAR1 and VAR3.

I am familiar with the Repeated Measure Least Square Means model for continuous variables, but I am struggling with the implementation of a similar approach for a Categorical outcome.

JMP 16.1, Windows

All inputs are welcome.

Best,

TS 

[#2]

Hi JMP Community,

After doing some reading, it seems that the Generalized Linear Model with a Binomial distribution is a reasonable approach to the analysis of longitudinal binary outcomes. However, I have a few questions regarding the details of the platform report:

1. In the Goodness of Fit: what is the correct interpretation when the Pearson Statistics is > 0.05 and the Deviance Statistics is < 0.05?
2. For the Studentized Deviance: what are the expectations for this distribution for a Binomial distribution?

Thank you for your help.

Best,

TS

[#3]

The Pearson chi square is the whole model test. The deviance is the lack of fit test, by comparison to the saturate model. The residual plot helps you find outliers or influential observations.