How does JMP remove inestimable model terms

[#1]

Dear community,

I want to evaluate the design of a data set with 12 binary main effects and 64 observations, and I decide to add all interaction effects (by selecting them under "factors" and clicking "interactions"->"2nd" under "Models"). JMP returns this message:

This design cannot fit the specified model. Inestimable model terms have been removed.

Now I know that 64 runs are not enough to estimate all main and interaction effects and that depending on multicollinearity in my data, JMP will choose a certain number of interaction terms that it can possibly estimate.

I am just curious as to what is the formula that JMP uses in order to determine how many (and which) interaction terms it can estimate.

Thank you in advance

[#2]

I do not understand how you could get this message in Custom Design. You specify the model terms before you make the design. The minimum number of runs is equal to the number of parameters that are necessary to estimate. You cannot enter a number of runs less than the minimum, which is 79 in this case. (1 intercept, 12 main effects, and N Choose K( 12, 2 ) = 66 two-factor interactions.

The design matrix containing the factor settings for each run is expanded to make the model matrix with a column for all the terms to be estimated. It is possible that some of the columns in the model matrix are the same. That means that two terms are aliases for the same estimation column. That means that their effects are confounded. The regression will detect confounding, which produces a singular matrix in solving for the parameter estimates, and report it as Singularity Details. Your example design produces many aliases in the model matrix with columns for all main effects and all interaction terms.

[#3]

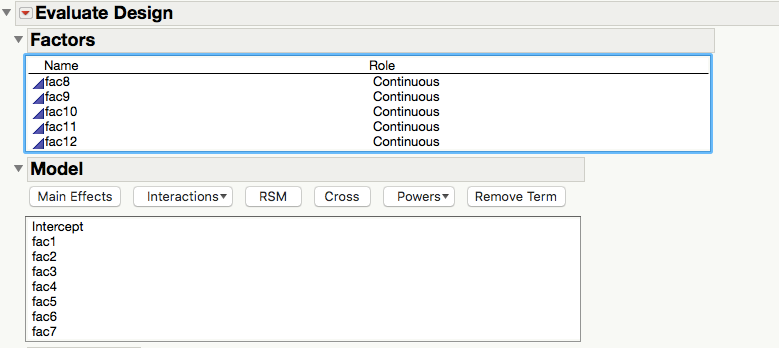
I was not specific enough  but my example works with the data set attached in the question. It is a question for the analysis stage and not the design stage. Once the data is open I select in the menu "DOE" --> "Design Diagnostics" -->  "Evaluate Design" and I add all interactions (see picture: I select all under "Factors" and under "Model", I add "interactions" --> "2nd". I then get the warning message. What is the exact formula that calculates the maximal number of interactions and how does JMP choose them? 

(it does not appear like it is an iterative process, since the message shows up very fast)

[#4 · Accepted solution]

That way makes sense. Evaluate Design uses the given design (64 runs) but you can evaluate designs for models other than the one for which it was designed.

The formula is simply the number of parameters to estimate. Your change to the model results in 79 parameters (1 intercept + 12 main effects + 66 two-factor interaction effects). (The number of interaction terms is the number of combinations of 12 factors chosen 2 at a time.) Your design provides 64 observations. So 15 parameters must be eliminated. That is one kind of deficiency of this design.

The second kind is the information provided by each run. As I explained, the regression process will expand the design matrix to make the model matrix. The column for estimating the intercept is a column of 1. The column for estimating the main effect of fac1 is the same as the data  column for fac1 in the design matrix. The column for estimating the interaction effect of fac1 and fac2 is the product (cross) of the data columns for these two factors, fac1*fac2. Some of the columns in the model matrix are the same. This case indicates that you have aliases for that estimation column. Your estimate is the linear combination of all the alias effects. The linear combination is based on the parameter values and the correlations among the aliases.

So you cannot have aliases in the regression analysis. Aliases produce a singularity in the regression solution. JMP eliminates terms that are aliases. That is, you can estimate one of the effects but not all of the aliases.It is impossible to determine which of the effects should be used from the design or the regression. JMP arbitrarily identifies the aliases to eliminate. It removes 15 terms from the end of the list, that is, the last 15 interaction effects.