- JMP will suspend normal business operations for our Winter Holiday beginning on Wednesday, Dec. 24, 2025, at 5:00 p.m. ET (2:00 p.m. ET for JMP Accounts Receivable).
Regular business hours will resume at 9:00 a.m. EST on Friday, Jan. 2, 2026. - We’re retiring the File Exchange at the end of this year. The JMP Marketplace is now your destination for add-ins and extensions.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- How does JMP determine the best model using AICc in stepwise regression?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
How does JMP determine the best model using AICc in stepwise regression?
How does JMP decide which combination of variables are the "best" model using forward AICc in the stepwise regression module? In other words, how does it decide when to stop, and why does it sometimes decide that there is no single "best" model? I've read that there must be a difference in AICc of 2 or greater, otherwise the models are considered equivocal. Is that what JMP is using also?
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Best model using AICc in stepwise regression
Hello,
When using the Minimum AICc stopping rule in Stepwise, the "best" model chosen should be the one with the smallest AICc value. I'm not sure that I have run across an example where Stepwise decides that there is no single best model.
However, the difference in AICc values from the minimum AICc value is important. According to Burnham & Anderson (2002; p. 70-71), a difference less than 2 implies substantial empirical support for he model with the higher AICc, a difference of 4 to 7 implies "considerably less" support for the model with the higher AICc, and a difference greater than 10 implies a level of empirical support that is "essentially none".
Regards,
Michael
Burnham & Anderson (2002), Model Selection and Multimodel Inference: A Practical Information Theoretic Approach. Springer, New York.
Link to publisher site: Model Selection and Multimodel Inference - A Practical Information-Theoretic Approach
Principal Statistical Writer
Manager, Statistical Documentation
JMP Development
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Best model using AICc in stepwise regression
Hi Benjamin,
I just wanted to add something regarding your question about when the Stepwise procedure stops and identifies a best model, with AICc as the stopping rule. When you click Go, the automatic fits (should!) continue until a Best model is found. The Best model is the one with a minimum AICc that can be followed by as many as ten models with larger values of AICc or BIC, respectively. In other words, the stepwise procedure tries to overcome local increases in AICc for as many as ten models, before deciding to terminate.
It appears that this rule was in place for JMP 11. So, in your example for PP13B, the smallest AICc value was for model 1. Then models 2 and 3 were fit, but their AICc values were greater than model 1's, and so the first model was selected as best. If it had been possible, JMP would have continued fitting another eight models, and would have settled on model 1 if none of those had a smaller AICc.
By the way, I was expecting that a fourth model that included Defleshing would be fit. But that didn't happen. I wonder if Defleshing and Field Dressing might be collinear, since they have the same SS values? (When model 3 was fit, stepwise could not fit a model 4.)
In your PP5-6 example, the model defined in Step 3 should have been identified as Best. I wonder again if there may have been a collinearity issue, causing stepwise to be unable to fit the next model. In any case, that third model should have been marked as Best.
I would strongly encourage you to try All Possible Models with your data. Using Stepwise in a Forward direction only considers models along a path defined by p-values, and this is only a subset of the possible models. By contrast, All Possible Models considers all models, with the limitation being the number of terms that you specify. With only four terms, you can easily fit all models, so you might find All Possible Models quite useful.
All Possible Models is a red triangle option in Stepwise. Once the All Possible Models report is generated, right-click in the body of the report and select Make into Data Table. Using the data table, you should construct a Graph Builder plot of AICc by Number (of parameters). Using this plot, you can easily see the tradeoff between smaller AICc and model complexity.
I hope this is useful...
Marie
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Best model using AICc in stepwise regression
Hello,
When using the Minimum AICc stopping rule in Stepwise, the "best" model chosen should be the one with the smallest AICc value. I'm not sure that I have run across an example where Stepwise decides that there is no single best model.
However, the difference in AICc values from the minimum AICc value is important. According to Burnham & Anderson (2002; p. 70-71), a difference less than 2 implies substantial empirical support for he model with the higher AICc, a difference of 4 to 7 implies "considerably less" support for the model with the higher AICc, and a difference greater than 10 implies a level of empirical support that is "essentially none".
Regards,
Michael
Burnham & Anderson (2002), Model Selection and Multimodel Inference: A Practical Information Theoretic Approach. Springer, New York.
Link to publisher site: Model Selection and Multimodel Inference - A Practical Information-Theoretic Approach
Principal Statistical Writer
Manager, Statistical Documentation
JMP Development
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Best model using AICc in stepwise regression
Hi Michael,
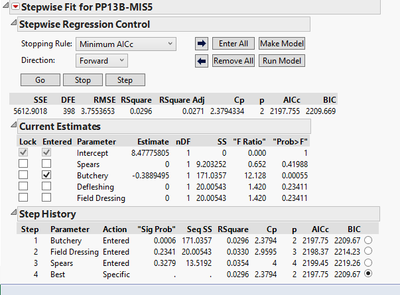
Thank you so much for your reply! I was familiar with the notion that a difference <2 suggested support for both models, but wasn't familiar with the 4-7 or >10. I wanted to show you a screen shot of what I'm talking about. In the first, JMP was able to find a "best" model using minimum AICc (the variables are an archaeological example I'm working on - using experimental tool use damage to predict prehistoric tool-use). You can see that the model with "butchery + intercept" is the best.
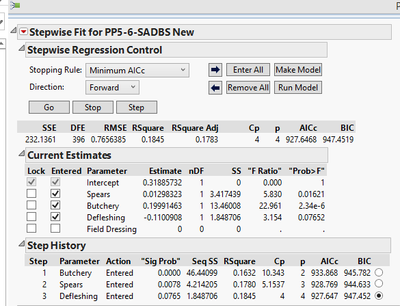
For this archaeological site, JMP did not find a "best" combination of experimental tool damage that fit the site:
I can see why it didn't find a "best" from the step history (difference <2 from previous step), but when it did find a "best" model in the prior screenshot, there was a difference <2 in the AICc of the two other model steps...I guess I'm just trying to figure out what it means when JMP finds a "best" versus when it doesn't.
Thanks,
Ben
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Best model using AICc in stepwise regression
Hi Ben,
I asked the tester for Stepwise about this, and she told me that it looked like you might have run into a bug that has been fixed for JMP12. If you'd like to send in your data, we could try it out with JMP12 to see if in fact you're running into that issue. Otherwise, you could wait to try it in JMP12 when it is released.
Thanks,
Michael
Principal Statistical Writer
Manager, Statistical Documentation
JMP Development
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Best model using AICc in stepwise regression
Hi Benjamin,
I just wanted to add something regarding your question about when the Stepwise procedure stops and identifies a best model, with AICc as the stopping rule. When you click Go, the automatic fits (should!) continue until a Best model is found. The Best model is the one with a minimum AICc that can be followed by as many as ten models with larger values of AICc or BIC, respectively. In other words, the stepwise procedure tries to overcome local increases in AICc for as many as ten models, before deciding to terminate.
It appears that this rule was in place for JMP 11. So, in your example for PP13B, the smallest AICc value was for model 1. Then models 2 and 3 were fit, but their AICc values were greater than model 1's, and so the first model was selected as best. If it had been possible, JMP would have continued fitting another eight models, and would have settled on model 1 if none of those had a smaller AICc.
By the way, I was expecting that a fourth model that included Defleshing would be fit. But that didn't happen. I wonder if Defleshing and Field Dressing might be collinear, since they have the same SS values? (When model 3 was fit, stepwise could not fit a model 4.)
In your PP5-6 example, the model defined in Step 3 should have been identified as Best. I wonder again if there may have been a collinearity issue, causing stepwise to be unable to fit the next model. In any case, that third model should have been marked as Best.
I would strongly encourage you to try All Possible Models with your data. Using Stepwise in a Forward direction only considers models along a path defined by p-values, and this is only a subset of the possible models. By contrast, All Possible Models considers all models, with the limitation being the number of terms that you specify. With only four terms, you can easily fit all models, so you might find All Possible Models quite useful.
All Possible Models is a red triangle option in Stepwise. Once the All Possible Models report is generated, right-click in the body of the report and select Make into Data Table. Using the data table, you should construct a Graph Builder plot of AICc by Number (of parameters). Using this plot, you can easily see the tradeoff between smaller AICc and model complexity.
I hope this is useful...
Marie
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us