- JMP will suspend normal business operations for our Winter Holiday beginning on Wednesday, Dec. 24, 2025, at 5:00 p.m. ET (2:00 p.m. ET for JMP Accounts Receivable).
Regular business hours will resume at 9:00 a.m. EST on Friday, Jan. 2, 2026. - We’re retiring the File Exchange at the end of this year. The JMP Marketplace is now your destination for add-ins and extensions.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: How do I compare 2 variances with an F-test?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
How do I compare 2 variances with an F-test?
Hello,
I need to compare the residual sum of squares in an unrestricted model with the residual sum of squares in a restricted model using an F-test to see if the additional independent terms in the unrestricted models significantly reduce the unexplained variations in the model. In the linked Youtube video, a guy shows how to do it manually (view the last 2 minutes or so) - however, I need to do it for a quite a few regressions, so it would be useful if there was a faster to do it in JMP.
Thanks in advance!
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How do I compare 2 variances with an F-test?
As Mark stated everything is available in JMP. You did not specify how these models are created. If you specify numerous Y responses for for the Complete model and then the same responses for the Reduced model this can save a lot of compute time. Assuming this is how the models are specified, here are the steps:
- Use Fit Model to specify the Complete model with numerous Y's.
- On any of the Analysis of Variance tables right click and select "make combined data table." This creates a table of the ANOVA results for each Y variable. Click in the corner and name this table "Complete."
- Repeat steps 1 & 2 for the reduced model and name this combined data table "Reduced."
- Bring the Complete table to the front, and select from the main menu Tables> Concatenate. Select Reduced and check the box for Create a Source column.
- Select a row with Error in the Source column, right click and select matching rows. Then invert the Row selection and delete rows ( or make a subset of the Error rows).
- Now split the table: Select columns :DF and :Sum of Squares for the Split columns, Split By :Source Table and Group By :Y, the responses. This table is now ready to compute the Partial F and the associated p-values in one column.
If you have 5 or more regressions that need this calculation and if the regressions are set up as assumed, it is worth while to follow these steps. However, it is not worth doing all 6 steps for numerous regressions.
If your numerous regressions are not run all at once, then create a table that looks like the one I attached below, using Copy and Paste for the DF and Sum of Squares, then create two new columns for the Partial F and P-value. And they can all be created at once. Note you can use the attached table. The Partial F and P-Value columns are formulas, so once the values are entered the F and significance are computed automatically.
I also attached a script. It is using only one response. But it would work for multiple Y's. Just in case you know some JSL.
BTW, the book Mark suggested is worth reading especially linear models or standard least squares.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How do I compare 2 variances with an F-test?
You do not need to run two models, with and without the predictor. Examine the Effect Test report for the model terms. There you will find the F test for each term, conditioned on the presence of the other terms. I believe that this information is all that you need to conclude if the term was significant per your guideline.
Following Georgia's advice, you can enter all of the response variables in the Y role along with the terms in the Effects list, click Run, then right-click on any one of the Effect Tests tables and select Make Combined Data Table. That action will give you one data table with the Effect Tests for all the responses.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How do I compare 2 variances with an F-test?
Do you have the data to fit the model in each regression? Then all you need is in Fit Least Squares platform reports.
If you only have the summarized regression quantities (e.g., sums of squares associated degrees of freedom), then you can use the F Distribution( ) function in a script editor with a log or a column formula.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How do I compare 2 variances with an F-test?
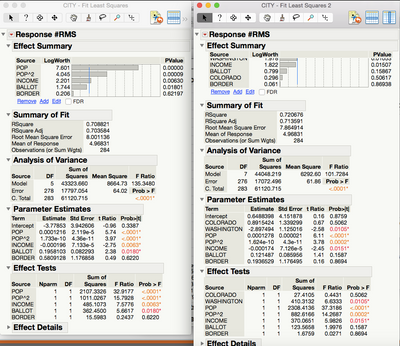
I do have the data to fit the model in each regression - but what exactly from the Fit Least Squares platform reports should I use? I have included the restricted and unrestricted model in the following screenshot.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How do I compare 2 variances with an F-test?
You do not need to run two models, with and without the predictor. Examine the Effect Test report for the model terms. There you will find the F test for each term, conditioned on the presence of the other terms. I believe that this information is all that you need to conclude if the term was significant per your guideline.
Following Georgia's advice, you can enter all of the response variables in the Y role along with the terms in the Effects list, click Run, then right-click on any one of the Effect Tests tables and select Make Combined Data Table. That action will give you one data table with the Effect Tests for all the responses.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How do I compare 2 variances with an F-test?
I should have added that you will find a lot of information by selecting Help > Books > Fitting Linear Models.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How do I compare 2 variances with an F-test?
As Mark stated everything is available in JMP. You did not specify how these models are created. If you specify numerous Y responses for for the Complete model and then the same responses for the Reduced model this can save a lot of compute time. Assuming this is how the models are specified, here are the steps:
- Use Fit Model to specify the Complete model with numerous Y's.
- On any of the Analysis of Variance tables right click and select "make combined data table." This creates a table of the ANOVA results for each Y variable. Click in the corner and name this table "Complete."
- Repeat steps 1 & 2 for the reduced model and name this combined data table "Reduced."
- Bring the Complete table to the front, and select from the main menu Tables> Concatenate. Select Reduced and check the box for Create a Source column.
- Select a row with Error in the Source column, right click and select matching rows. Then invert the Row selection and delete rows ( or make a subset of the Error rows).
- Now split the table: Select columns :DF and :Sum of Squares for the Split columns, Split By :Source Table and Group By :Y, the responses. This table is now ready to compute the Partial F and the associated p-values in one column.
If you have 5 or more regressions that need this calculation and if the regressions are set up as assumed, it is worth while to follow these steps. However, it is not worth doing all 6 steps for numerous regressions.
If your numerous regressions are not run all at once, then create a table that looks like the one I attached below, using Copy and Paste for the DF and Sum of Squares, then create two new columns for the Partial F and P-value. And they can all be created at once. Note you can use the attached table. The Partial F and P-Value columns are formulas, so once the values are entered the F and significance are computed automatically.
I also attached a script. It is using only one response. But it would work for multiple Y's. Just in case you know some JSL.
BTW, the book Mark suggested is worth reading especially linear models or standard least squares.
Recommended Articles
- © 2025 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us