- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: How JMP calculate confidence interval for a linear fit model
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
How JMP calculates confidence interval for a linear fit model
For the following set of data,
| X | Y |
| 7.9 | 115 |
| 13 | 154 |
| 10.8 | 156 |
| 11.6 | 182 |
| 10.5 | 124 |
| 11.1 | 157 |
| 8.8 | 129 |
| 11.9 | 181 |
| 11.1 | 164 |
| 9 | 122 |
| 7.4 | 100 |
| 6.9 | 86.2 |
| 9.4 | 118.9 |
| 7.2 | 94.2 |
| 8.8 | 114.3 |
| 7.1 | 104.9 |
| 12.4 | 181.5 |
| 12.1 | 166.1 |
| 15.1 | 166.1 |
| 14.2 | 157.7 |
one can generate a linear fit model as shown below:
Linear Fit
Y = 24.522739 + 11.068566*X
Summary of Fit
RSquare 0.743712
RSquare Adj 0.729474
Root Mean Square Error 16.17783
Mean of Response 138.695
Observations (or Sum Wgts) 20
The question I have is: how should I go about and generate the 99% confidence intervals for the projected Y when X = 11.8 and 12.7? Or even better if you could elaborate the details on how JMP calculates the confidence intervals (such as, 95%, 99%) for a linear fit model.
Many thanks in advance!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How JMP calculate confidence interval for a linear fit model
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How JMP calculate confidence interval for a linear fit model
The covariance matrix for the estimates is not provided in the JMP reports for Bivariate or Fit Least Squares. (Fit Least Squares provides an optional report about the correlation of the estimates, but that information is not what you want.) It is not available through a menu command, either. It is available as the first argument to the Vec Quadratic() function when you save the formula for confidence intervals, as you already discovered.
All of the textbooks about linear regression methods that I know of cover the linear model, parameter estimation, interval estimation, covariance of the estimates, and more. I am sure that much of the same information is available on reliable Web sites if you don't have or do not want to procure one of these textbooks.
Given that you are using JMP and JMP already provides these intervals graphically and numerically, I don't understand why you want to go through of the explicit computations.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How JMP calculate confidence interval for a linear fit model
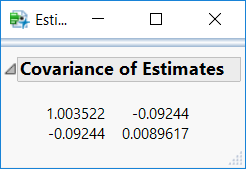
Here is a script that demonstrates how the covariance of the estimates is computed using your sample of data.
Names Default to Here( 1 );
// make example into data table
dt = New Table( "Example for CI in Regression",
Add Rows( 20 ),
New Column( "X",
Numeric,
"Continuous",
Format( "Best", 12 ),
Set Values(
[7.9, 13, 10.8, 11.6, 10.5, 11.1, 8.8, 11.9, 11.1, 9, 7.4, 6.9, 9.4, 7.2,
8.8, 7.1, 12.4, 12.1, 15.1, 14.2]
)
),
New Column( "Y",
Numeric,
"Continuous",
Format( "Best", 12 ),
Set Values(
[115, 154, 156, 182, 124, 157, 129, 181, 164, 122, 100, 86.2, 118.9,
94.2, 114.3, 104.9, 181.5, 166.1, 166.1, 157.7]
)
)
);
// perform regression analysis
fls = dt << Fit Model(
Y( :Y ),
Effects( :X ),
Personality( "Standard Least Squares" ),
Emphasis( "Minimal Report" ),
Run(
:Y << {Summary of Fit( 1 ), Analysis of Variance( 1 ),
Parameter Estimates( 1 ), Plot Actual by Predicted( 0 ),
Plot Residual by Predicted( 0 ), Plot Studentized Residuals( 0 ),
Plot Effect Leverage( 0 ), Box Cox Y Transformation( 0 )}
)
);
// obtain model matrix x
xx = fls << Get X Matrix;
// compute covariance matrix of parameter estimates
cov est = Inverse( xx` * xx );
// display covariance matrix
New Window( "Estimates Covariance",
Outline Box( "Covariance of Estimates",
Matrix Box( cov est )
)
);
The first part of the script produces a data table with the data that you first provided. I use the Fit Least Squares platform to get the regression model matrix but it could also be made using matrix operations. Then it computes and displays the covariance matrix.
You should recognize this matrix as the first argument in the Vec Quadratic() function in the column formula that you saved.
The covariance matrix is the inverse of the information matrix for the parameters, which, in turn, is the Transpose( XX ) * XX, where XX is the model matrix. XX has a column for every term in the linear model. In your example, the frist column is 1 to estimate the intercept (constant response) and the second column is the X data column from the data table (your predictor). If you included the quadratic term, the third column of XX would be X^2, and so on. The response column Y is not involved.
I hope that this example illustrates what the covariance matrix is and where it comes from.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How JMP calculate confidence interval for a linear fit model
This forum is wonderful!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How JMP calculate confidence interval for a linear fit model
Yes, I can show you how JMP performs the Vec Quadratic() calculation. Here is a direct excerpt from the guide:
Select Help > Books > Scripting Guide. Then press CTRL-F and enter "quadratic(" for the search string. Very easy.
Using the same simple technique, I found the answer to your next question:
This entry is right above the one for Vec Quadratic().
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How JMP calculate confidence interval for a linear fit model
Second answer:
- No, it is not more appropriate to use the prediction interval if you are estimating or testing the expected value (or mean) of the response with an interval.
- Yes, it is more appropriate to use the prediction interval if you are estimating a proportion of the population.
They are both correct and both appropriate, depending on what you want to estimate or test. They answer different questions. They are not used for the same purpose. The former is for the statistic and the latter is for the data.
BTW, you can easily visualize either one or both of these intervals when you fit the line in Bivariate. Use same menu under the plot and select Confid Shaded Fit or Confid Shaded Indiv. One is related to the uncertainty in the sample statistic (regression line) and the other is related to the uncertainty of individual observations.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How JMP calculate confidence interval for a linear fit model
Thanks for the detailed explanation!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How JMP calculate confidence interval for a linear fit model
I think my JMP is an old versiont (10.0) so that in my drop down menu it does not have ""Mean Confidence Limit formula" or "Indiv Confidence Limit Formula". Any suggestion how to get those Y+CI and Y-CI numbers? Thanks!
- « Previous
-
- 1
- 2
- Next »
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us