- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Generating conditional and marginal R-squared for mixed models
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Generating conditional and marginal R-squared for mixed models
I am running a series of mixed models in JMP 16 (one random effect, multiple fixed effects).
I would like to generate estimates of:
- Marginal R^2 (R^2m): the proportion of variance explained by the fixed effects relative to the overall variance
- Conditional R^2 (R^2c): the proportion of variance explained by both fixed and random effects relative to the overall variance
Is there a script readily available?
In addition, how does JMP compute the R^2 and adjusted R^2 in the "Summary of Fit" tab in the Fit Model report for a mixed model?
Note regarding conditional and marginal R^2: The method proposed by Nakagawa & Schielzeth (2013) applies to random intercept models. Johnson (2014) proposed an extension for models that include random slopes (see also Nakagawa, Schielzeth, & Johnson 2017).
Johnson, P. C. D. 2014. Extension of Nakagawa & Schielzeth’s R2GLMM to random slopes models. Methods in Ecology and Evolution 5: 944–46. doi:10.1111/2041-210X.12225.
Nakagawa, S., & H. Schielzeth. 2013. A general and simple method for obtaining R2 from generalized linear mixed-effects models. Methods in Ecology and Evolution 4(2): 133–42. doi:10.1111/j.2041-210x.2012.00261.x.
Nakagawa, S., H. Schielzeth, & P. C. D. Johnson. 2017. The coefficient of determination R2 and intra-class correlation coefficient from generalized linear mixed-effects models revisited and expanded. Journal of the Royal Society Interface 14(134). doi:10.1098/rsif.2017.0213.
- Tags:
- windows
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Generating conditional and marginal R-squared for mixed models
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Generating conditional and marginal R-squared for mixed models
Yes, I did, but I did not see reference to conditional or marginal R-squared, nor do I see where I can obtain the variance terms needed to compute the two statistics. For example, see this explanation for scripting in R: Marginal and Conditional R2 for Linear Mixed Models in JAGS (samcarcagno.altervista.org)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Generating conditional and marginal R-squared for mixed models
I think all the information are available in Mixed Model report. But it may require substantial knowledge to identify and collect them. I will give it a try. I use JMP sample data Animals as an example.
Part 1
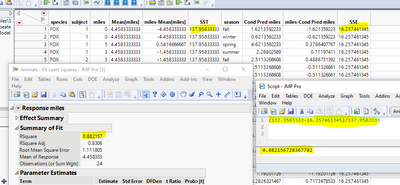
To answer how JMP gets R^2. Run the script embedded in the data table to bring up the report. And go to platform menu and use "Save Columns" -> "Conditional Pred Values" to save predictions. Now you get R^2 the same way as you get one from a linear least square model. Formula is here Summary of Fit . E.g. you need responses and predictions to get residuals and calculate sum of squares of errors SSE; you need responses and their mean to calculate sum of squares of total SST. Then R^2 is (SST - SSE)/SST. And here is my proof of calculation:
Part 2
Now answer your remaining questions. You need sigma_f^2, sigma_a^2, and sigma_e^2.
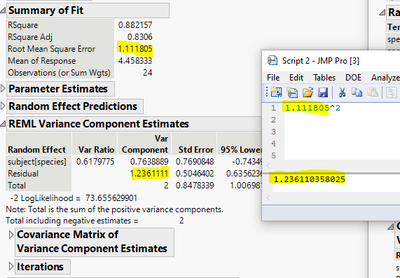
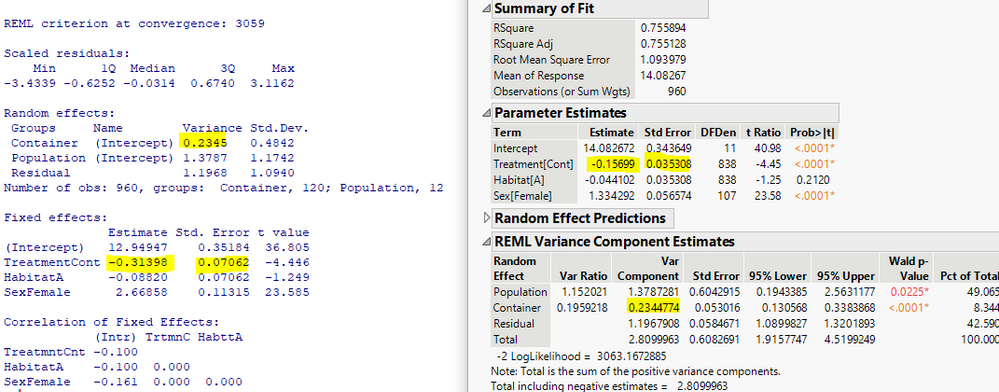
You can find sigma_e in Summary of Fit. It is Root Mean Square Error.
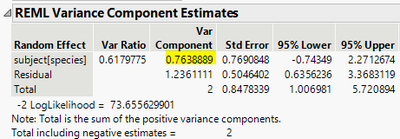
You can find sigma_e^2 in REML Variance Component Estimates. It is the Var Component associated with Residual.
Here is the proof of their relationship:
You can find sigma_a^2 in REML Variance Component Estimates. It is the Var Component associated with the random effect. For this example, there is just one component:
Now comes to sigma_f^2. This may require substantial knowledge of linear model. You may need to consult some textbooks to understand why so in the following steps. Here are the steps.
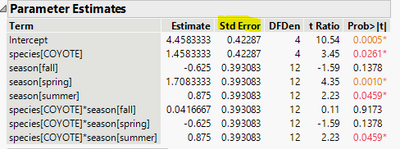
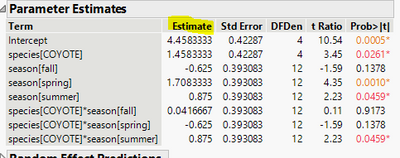
You need Std Error of the fixed parameter estimates, and put them in a diagonal matrix called Matrix_S, with these Std Error on the diagonal.
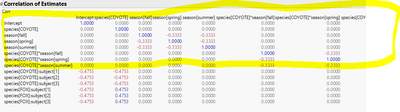
You need the correlation matrix of the fixed parameter estimates. You can find it by going to the platform menu "Estimates" > "Correlation of Estimates". But you don't need all of it, just the upper left square portion that is associated with fixed parameters. Put this portion of matrix in a matrix called Matrix_R.
Now you need linear algebra to calculate the product of Matrix_S, Matrix_R, and Matrix_S again to get a new matrix. The result is the covariance matrix of the fixed parameters, call it COV. For these matrix operations, this page might be helpful: Converting a Correlation Matrix to a Covariance Matrix
Now you need Parameter Estimates again, this time, the Estimate part. Put them in a row vector, call it VECTOR.
Now, more linear algebra. you need to calculate VECTOR * COV * transpose(VECTOR). You have your sigma_f^2.
Now you have all three pieces. The rest calculation is the easy part. But it may require quite some effort to write a script to do it automatically.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Generating conditional and marginal R-squared for mixed models
Thank you very much for taking the time to provide a detailed explanation (and the associated visuals).
Unfortunately, I think the linear algebra steps needed to compute the sigma_f^2 component is beyond me.
Thanks again!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Generating conditional and marginal R-squared for mixed models
From a hindsight, if the reference paper has a data set and model, and gives their results, may I suggest the following?
Use their data set and fit their model in JMP. You get a JMP R^2. Compare JMP R^2 with their conditional R^2.
Then, following the same steps above of calculating JMP R^2, but instead of using "Conditional Pred Values", you use "Predicted Values" under "Save Columns" menu, and calculate a different R^2, call it R*^2. Compare R*^2 with the marginal R^2 in the paper.
Look how close the comparisons are. If you can do those, please post back what you find to let the community readers know. Thanks!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Generating conditional and marginal R-squared for mixed models
Thank you. They do appear to offer a data set in the appendix of the manuscript. I will see if I can retrieve it and run the tests that you suggest.
I will let you know what transpires. Again, thank you for your input.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Generating conditional and marginal R-squared for mixed models
Hello again,
I tried running the "size model" data from Nakagawa through the mixed modeling procedure in JMP (via mixed model or SLS w/ REML). The output resulted in similar variance components for the random effects and similar AIC, BIC values, but the coefficients for the fixed effects differed from those in the Nakagawa paper (see Table 3 in the attached pdf). Might this be because R and JMP use a different base condition for the coefficients of the 3 categorical treatments (e.g., males instead of females)?
The R^2 from JMP (0.755) was fairly similar to the conditional R^2 in the paper (0.741), but not quite the same. I generated a column of predicted values from the JMP model and regressed those against the raw data (if I understood your suggestion correctly). This produced an R^2 (0.402) fairly similar to their marginal R^2 (0.392), but again, not quite the same. Do you have thoughts on these differences?
I have attached the Nakagawa paper and the imported data file -- the latter with two additional columns: the predicted and conditional predicted values.
If you wish to explore the data further, please do so. I will be interested to learn more.
Thank you, again.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Generating conditional and marginal R-squared for mixed models
You did correctly! And I am able to match JMP and R results. The differences that you see is due to differences between design matrix coding conventions.
Here is the screenshot of results side by side. First, variance components completely match. Second, JMP fixed effect parameter estimates (except intercept) are exactly half of those from R. Std Error is also by half. R use (0, 1) coding for binary X variables, JMP use (-1, 1) coding for binary X variables.
I am not able to verify the proposed R^2 numbers in the paper using the numbers that I see here, regardless from JMP numbers or R numbers. I kind of lost about what they have done. I notice that the GLMM versions of their R^2 are reported, which involves sigma_d^2, which I don't understand what it is, it's in a separate paper. Maybe that is the missing piece. In addition, JMP reports a slight correlation between random effects. The paper does not consider correlation among random effects. This maybe a second missing piece.
The R^2 that JMP produces and the other one that I suggested are conceptually similar to what they want to achieve. But I cannot figure out how to get their numbers. I am glad the numbers are rather close.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Generating conditional and marginal R-squared for mixed models
Thanks. That makes sense re: the fixed effects coefficients (although I don't understand the difference in the intercept).
Here is a web site that explains the calculation and components of R^2(m) and R^2(c)
https://jonlefcheck.net/2013/03/13/r2-for-linear-mixed-effects-models/
It describes the last two terms in the denominator as follows: " ... the last two terms add up the residual variance and are the additive dispersion component (for non-normal models) and the distribution-specific variance". Not sure what this means.
Do you think these explain the small difference (i.e., they are minor adjustments)?
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us