- JMP will suspend normal business operations for our Winter Holiday beginning on Wednesday, Dec. 24, 2025, at 5:00 p.m. ET (2:00 p.m. ET for JMP Accounts Receivable).
Regular business hours will resume at 9:00 a.m. EST on Friday, Jan. 2, 2026. - We’re retiring the File Exchange at the end of this year. The JMP Marketplace is now your destination for add-ins and extensions.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Generalized Linear Models without intercept
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Generalized Linear Models without intercept
Hi,
I need your help. I want to make an anaylsis with GLM, but without intercept. I can't choose the option "No intercept".
I want to get the same results like there: http://support.sas.com/kb/24/992.html
I have no idea, how the get the option "No Intercept" in GLM, distribution=Binomial, Link=Logit
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Generalized Linear Models without intercept
Hi @mhans,
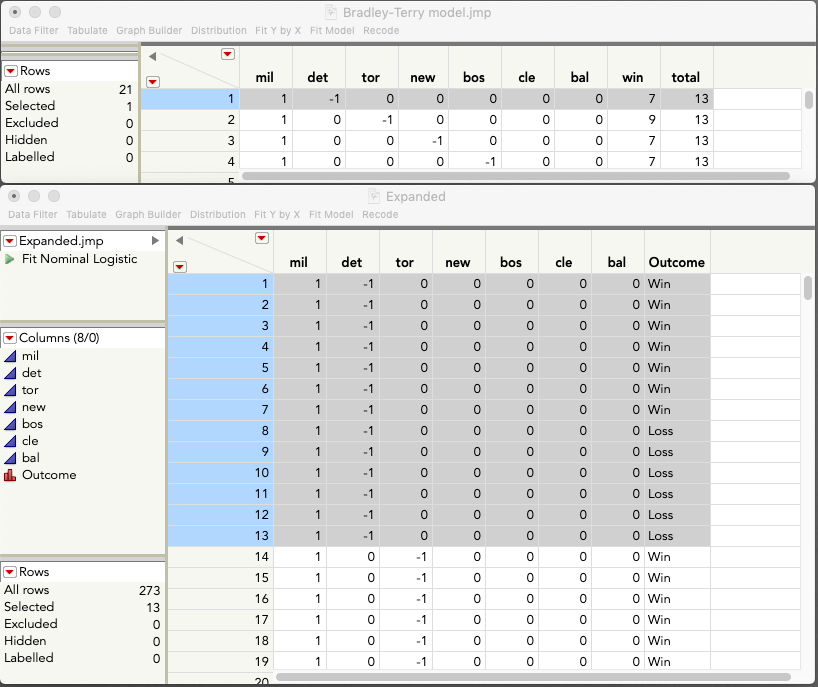
It is possible in standard JMP, but it requires a slight restructuring of your table. What you need is a nominal outcome variable of Win or Loss, and what you have is a summarized table of the frequencies of those occurrences. I've attached such an expanded table here, with the nominal logistic script saved (discussed below more). Note the form of these tables, in the image below is the original table with the first row selected, in the bottom is the expanded table, with the 13 rows selected that correspond to that one summarized row. Note there are 13, which are the 13 contests between Mil and Det, and there are 7 wins, and 6 losses, which reflect the win = 7 in the top table.
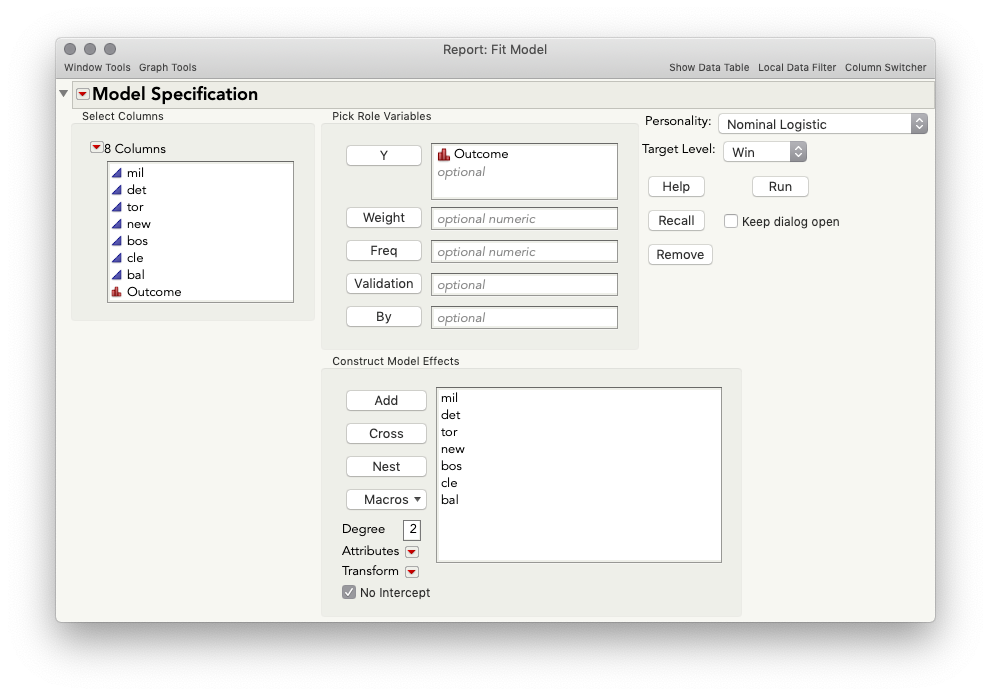
The model is straightforward to set up: Analyze > Fit Model, with Outcome as Y, all the teams as model effects, and No Intercept checked.
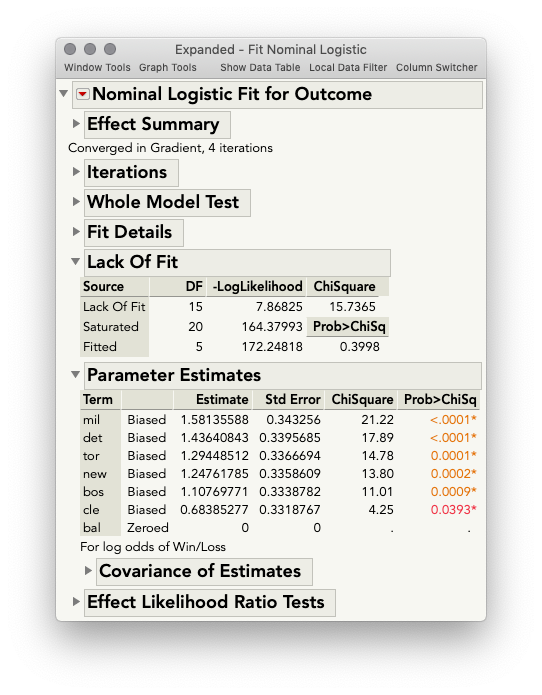
This returns the following output, which you will see matches:
Fit Model(
Y( :Outcome ),
Effects( :mil, :det, :tor, :new, :bos, :cle, :bal ),
No Intercept( 1 ),
Choose High Target( 1 ),
Personality( "Nominal Logistic" ),
Run( Likelihood Ratio Tests( 1 ), Wald Tests( 0 ) ))The value-add of Generalized Regression here is that you can directly specify the win/total structure when defining your y variable, which handles the expansion in the background.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Generalized Linear Models without intercept
Hi @mhans,
Unlike the Generalized Linear Model personality, the Nominal Logistic personality in Fit Model can be run without an intercept by checking the box "No Intercept" in the Fit Model dialog window. This personality will return equivalent results to the Generalized Linear Model personality with a binomial error distribution and logit link function, assuming you haven't checked the Firth Bias-Adjusted estimates (with this box checked the model estimates will differ). Perhaps this will work for your situation?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Generalized Linear Models without intercept
Hi @julian,
thanks for your reply. I tired to use the nominal logistic personality. The response variable y should be nominal, my variable y was metric (between 0 and 1, a percentage of wins). I made a new structur for my data with the variable y: 1 or -1 and I copied the data in the form
1 -1 0 0 0 0 0 7 1 1 0 -1 0 0 0 0 9 1 (...) 0 0 0 0 0 1 -1 6 1
(new part of data)
-1 1 0 0 0 0 0 6 -1
-1 0 1 0 0 0 0 4 -1
(...)
0 0 0 0 0 -1 1 7 -1
The results are not the same like in SAS. I have no idea, how to repear it...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Generalized Linear Models without intercept
Hi @mhans,
I better understand what you're trying to do now. To match those results (Bradley-Terry model) you will need to use the Generalized Regression platform, which is available in JMP Pro only. I've attached a JMP version of the data table used in that SAS example and saved the script to the table. Here are the steps to reproduce this:
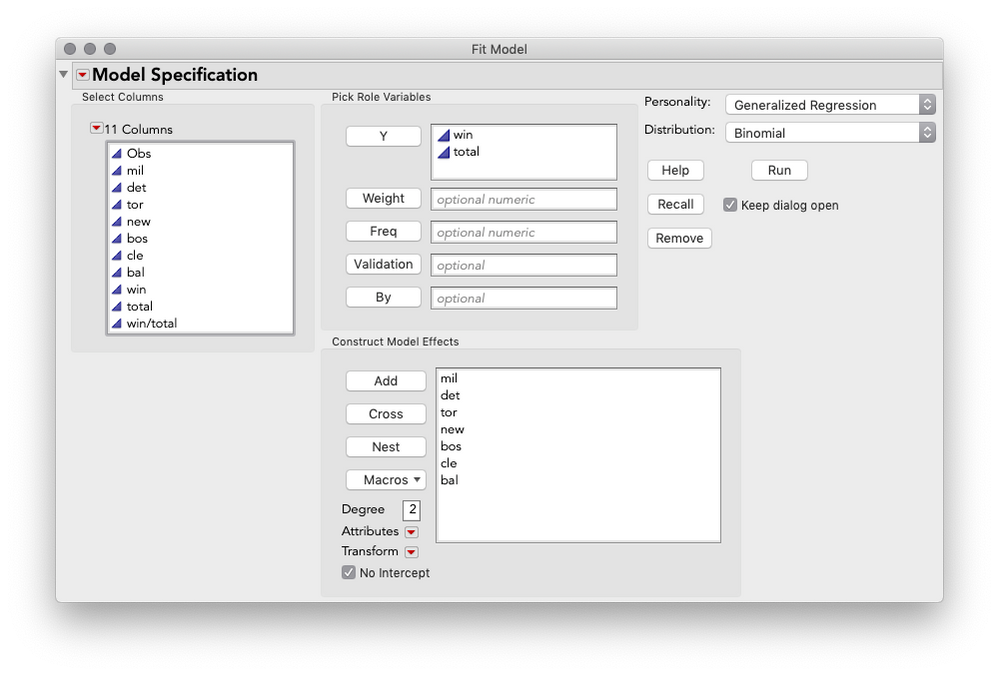
1. Launch Analyze > Fit Model.
2. Specify Generalized Regression as the Personality, and Distribution as Binomial.
3. Enter both Win and Total as Y, Columns, and enter all predictors as model effects.
4. Check "No Intercept" at the bottom.
Your Fit Model dialog should now look like this:
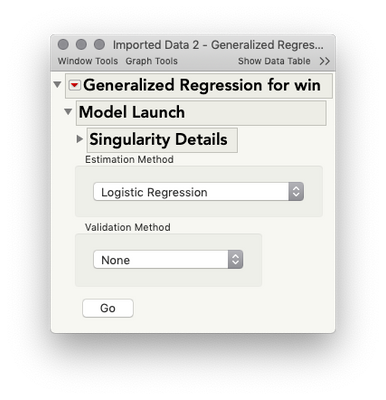
5. Click Run, then in the resulting dialog, specify Logistic Regression as the estimation method, and click go:
This will return the following output, which you can confirm matches the SAS results.
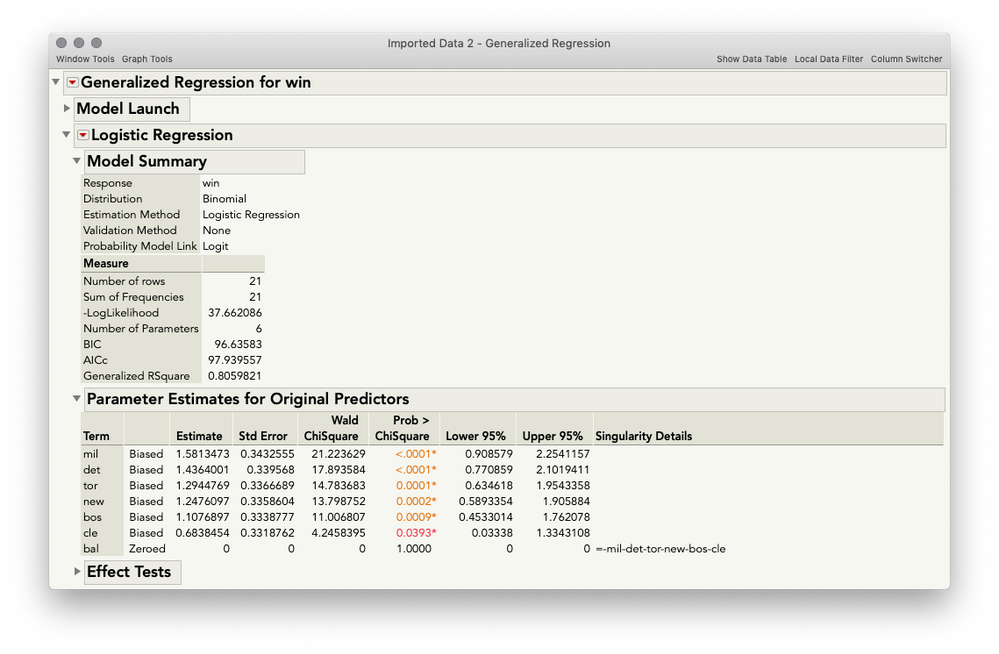
Fit Model(
Y( :win, :total ),
Effects( :mil, :det, :tor, :new, :bos, :cle, :bal ),
No Intercept( 1 ),
Personality( "Generalized Regression" ),
Generalized Distribution( "Binomial" ),
Run(
Fit( Estimation Method( Logistic Regression ), Validation Method( None ) )
)
);
I hope this helps!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Generalized Linear Models without intercept
Hi @julian,
wow, thnank you! I am seeing, it is possible in JMP. I have only the "normal" version of JMP. Is it possible to do this model with the normal version (as logistic regression without intercept or GLM)?
If no, can you send me the output in the pdf.-form?
Hats off for this solution.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Generalized Linear Models without intercept
Hi @mhans,
It is possible in standard JMP, but it requires a slight restructuring of your table. What you need is a nominal outcome variable of Win or Loss, and what you have is a summarized table of the frequencies of those occurrences. I've attached such an expanded table here, with the nominal logistic script saved (discussed below more). Note the form of these tables, in the image below is the original table with the first row selected, in the bottom is the expanded table, with the 13 rows selected that correspond to that one summarized row. Note there are 13, which are the 13 contests between Mil and Det, and there are 7 wins, and 6 losses, which reflect the win = 7 in the top table.
The model is straightforward to set up: Analyze > Fit Model, with Outcome as Y, all the teams as model effects, and No Intercept checked.
This returns the following output, which you will see matches:
Fit Model(
Y( :Outcome ),
Effects( :mil, :det, :tor, :new, :bos, :cle, :bal ),
No Intercept( 1 ),
Choose High Target( 1 ),
Personality( "Nominal Logistic" ),
Run( Likelihood Ratio Tests( 1 ), Wald Tests( 0 ) ))The value-add of Generalized Regression here is that you can directly specify the win/total structure when defining your y variable, which handles the expansion in the background.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Generalized Linear Models without intercept
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us