So, I would like to find the Area under some curves. Actually quite many of them, so using the Trapezoid method manually won't work, and can't imagine it would be valid enough. There is some kind of function for this for ROC-curves, but is it usable for finding the AUC in curves, measureing blood substances over time (five times)?
However, if I get a formula for a fitted Curve, I can use it to find AUC (Integral) in other software. For example, a Sixth degree polynomial. Here, I get the the function but I can't make sense of it (pic 1).
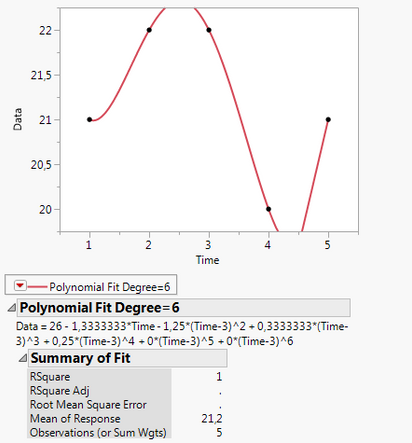
Polynomial functions are:
But I can't make sense of the Formula JMP provides me. Using only Time=3?
By using a flexible smoothing spline fit, I can get some coeffecients, but those won't help me (pic 2)?
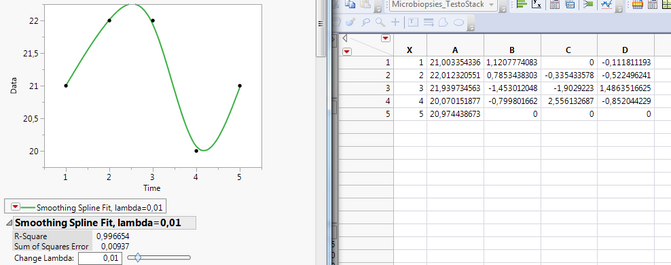
Would be grateful for tips getting the equation integral-ready and/or finding the AUC easily, for many subjects/curves.