- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Formula for polynomial function / Finding Area under the Curve
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Formula for polynomial function / Finding Area under the Curve
So, I would like to find the Area under some curves. Actually quite many of them, so using the Trapezoid method manually won't work, and can't imagine it would be valid enough. There is some kind of function for this for ROC-curves, but is it usable for finding the AUC in curves, measureing blood substances over time (five times)?
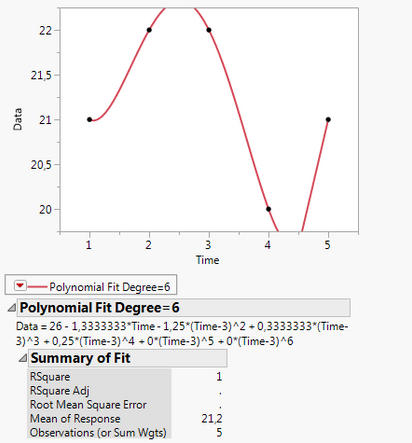
However, if I get a formula for a fitted Curve, I can use it to find AUC (Integral) in other software. For example, a Sixth degree polynomial. Here, I get the the function but I can't make sense of it (pic 1).
Polynomial functions are:
But I can't make sense of the Formula JMP provides me. Using only Time=3?
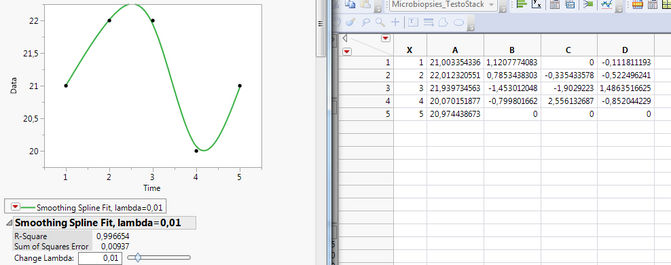
By using a flexible smoothing spline fit, I can get some coeffecients, but those won't help me (pic 2)?
Would be grateful for tips getting the equation integral-ready and/or finding the AUC easily, for many subjects/curves.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Formula for polynomial function / Finding Area under the Curve
the Fit Special dialog has a check box for centering.
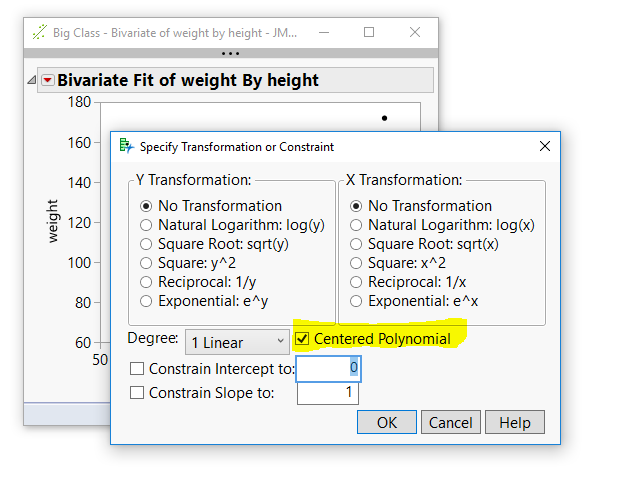
It looks like this dialog stops at degree 5.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Formula for polynomial function / Finding Area under the Curve
You should still be able to work with the equation in this form. But if you must have an uncentered form you can save the prediction formula, open the formula in the formula editor, and select the simplify option under the red triangle menu.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Formula for polynomial function / Finding Area under the Curve
Thank you. Hmm so "26 - 1,3333333*Time - 1,25*(Time-3)^2 + 0,3333333*(Time-3)^3 + 0,25*(Time-3)^4 + 0*(Time-3)^5 + 0*(Time-3)^6" would be the predicted formula? Will try.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Formula for polynomial function / Finding Area under the Curve
Ok, seems like I had to change the commas to dots, then I got something out of it.
(Forth degree, not sixth, would be enough btw)
First: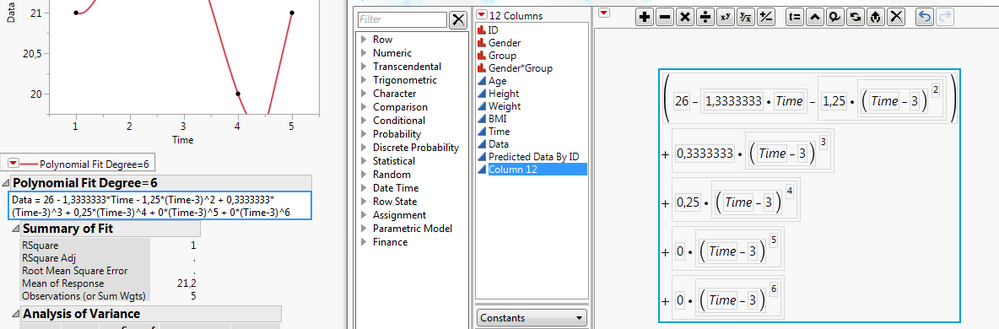
Hm is that a valid polynomial function? Having trouble integrating it atleast.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Formula for polynomial function / Finding Area under the Curve
the Fit Special dialog has a check box for centering.

It looks like this dialog stops at degree 5.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Formula for polynomial function / Finding Area under the Curve
Ah! Yeah, thank you.
Now I got the formula looking like: 26 - 11,833333*Time + 9,25*Time^2 - 2,6666667*Time^3 + 0,25*Time^4
Will try to exchange Time for X and integrate..
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Formula for polynomial function / Finding Area under the Curve
However a little time consuming for multiple curves but could do. Thank you!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Formula for polynomial function / Finding Area under the Curve
You only have to symbolically integrate the polynomial once, then evaluate it with different sets of fitted parameter estimates.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Formula for polynomial function / Finding Area under the Curve
Hmm. I'm about to compare the mean-AUC for some parameters, for 20 subjects divided into two groups.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Formula for polynomial function / Finding Area under the Curve
Anyone wondering about the centering: I think it helps numerical accuracy, potentially a lot. JMP uses double precision floating point numbers that can represent 15-16 digits. In this example you can see the two formulas agree to about 9 digits.
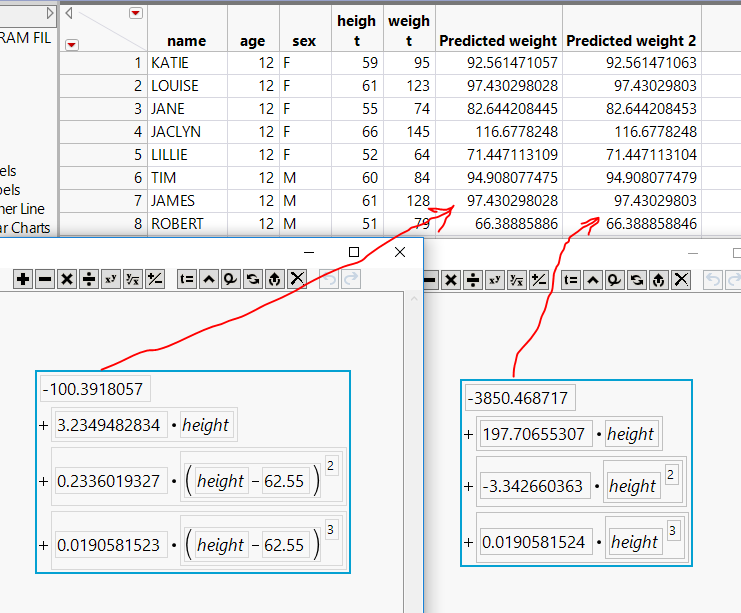
For Katie (row 1) the calculations look like this:
| term | centered | uncentered |
| ^0 | -100.391805727981 | -3850.46871657937 |
| ^1 | 190.861948723194 | 11664.6866311208 |
| ^2 | 2.9439683570111 | -11635.8007229098 |
| ^3 | -0.852640295610253 | 3914.14427943114 |
| Sum | 92.5614710566141 | 92.5614710627333 |
For the uncentered column, the most significant digits in all of the terms are much bigger than the sum, and those most significant digits mean there is no room to represent more least significant digits.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us