Fit Model Results Issue

[#1]

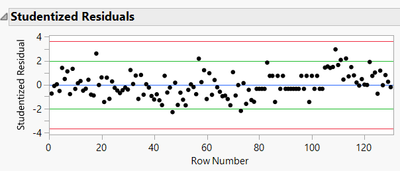
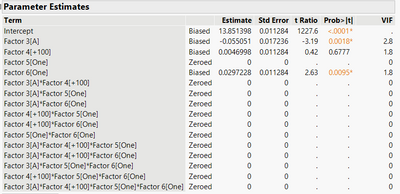
JMP 17: I have a few general questions about the results I obtained from a Fit Model platform analysis. I am attaching my data set. I have one response continuous variable, Thickness and four categorical factors that were modulated, two levels each. Thickness was used as the Y Variable and all four Factors (3, 4, 5 & 6) were moved into the Construct Model Effects area by selecting Macro > Factorial Sorted. I am interested in seeing if there are any interactions. In the results, the first thing I notice is that the Studentized Residuals plot has a sinusoidal pattern. I watched a JMP video where the presenter mentioned that if there is a pattern in this residuals plot there may be an issue with the data? Next, the Parameter estimates table has several rows having no results. What is this indicating? Likewise the Effect Tests table has no data either. What is this indicating? Any inputs would be appreciated. I searched for articles or videos but haven't come across any similar issues.

Thank you.

[#2]

The cyclic pattern is evident in the residual plot. Just to be sure, the rows in the table occur in the same order as the actual runs?

The zero estimates indicate that you over-specified the model. You designed the experiment for a simpler model and then added higher-order terms during analysis, but the design (data) do not support estimating all the terms. It is not a matter of the number of runs. You could design a 4-factor, 2-level experiment to estimate the 4 main effects and the intercept in just 5 runs. You could replicate this design many times for a large number of total runs, but you still can't estimate higher-order effects.

In your case Factor 3 = B was only run at one level of the other factors.

[#3]

Mark, thank you for the response. The rows in the table are not in run order. The experiments were performed on parts that have several process steps. So the four Factors listed were at different process steps. The Factors are numbered in the process order in which they occurred.

A bit more detail, I was not involved in the design of this experiment. I believe this was not a true DOE setup. Basically a multi-factor two level matrix experiment. Does this preclude using the Fit Model platform to analyze the results?

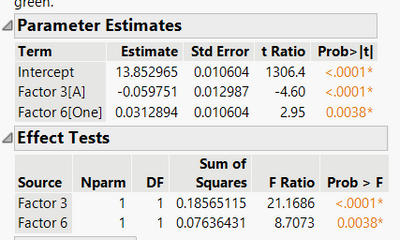
I tried using the Add method for the Factors in the Construct Model Effects area, I didn't use the Macro option for factorials, the result is below. I removed Factors 4 & 5 then reran the analysis. So Factors 3 Level A & 6 Level One are showing statistically significant deltas to their opposite levels? What is the significance of the Intercept?

[#4]

It would be a good idea to determine the run order and sort the table in run order to investigate the cyclic pattern observed in the residuals.

The fact that the four factors are involved in different process steps means that the experiment is not randomized. This fact has important implications for the analysis of the data. The statistical errors are correlated. The fundamental assumption of constant variance across the response range is likely violated. The model with a single constant variance is inadequate. The parameter estimates for the effects of each factor require different standard error calculations based on the multiple experimental units (randomization). Otherwise, the type I and type II errors are different than expected, and p-values do not have the expected coverage.

All t-tests in the Parameter Estimates table are (estimated parameter - hypothesized parameter) / (standard error of estimate). The hypothesized parameter value is zero. So the intercept is compared to zero, like the other parameters. The standard errors, however, are unlikely to be correct because of the split-plot 'design' used to collect the data.