- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Failing Normality Test
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Failing Normality Test
Dear all,
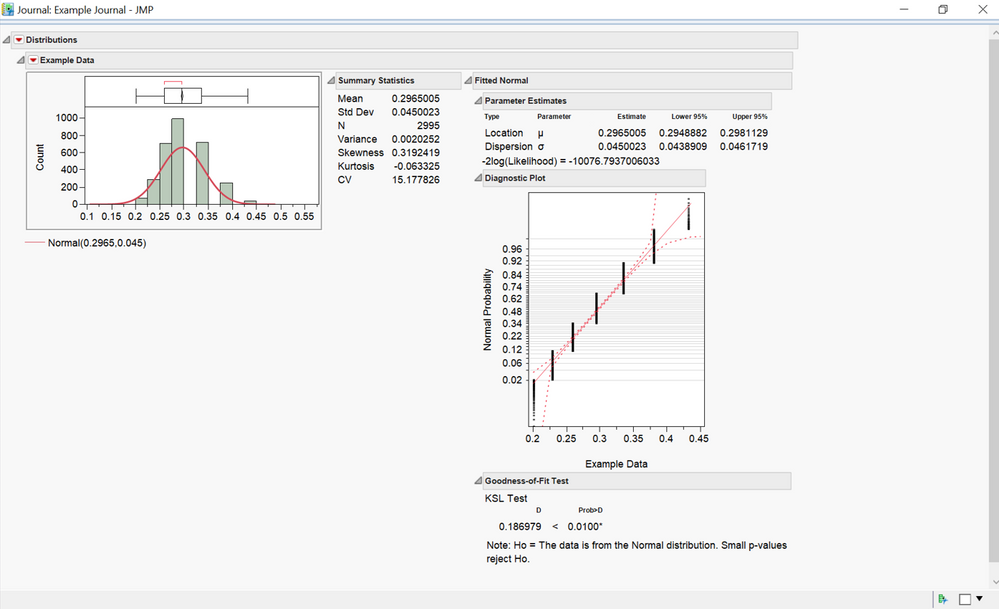
I am trying to perform a normality test on a series of datasets similar to the one shown in the figure attached, and later compare them using ANOVA. However, when I perform the normality test, I keep getting what I considered to be a ‘false negative.’ As you can see from the screenshot of the journal, the dataset as a whole resembles a normal distribution, even though there are only about 7-8 bins being populated. My best guess is that because there are ‘so many’ empty bins in between the populated ones, JMP is interpreting the dataset as multimodal. I would like it to perform the fit/test on the overall set as shown graphically.
However JMP is interpreting the distribution of the data, it also affects the conclusions drawn from ANOVA. I would be very grateful if anyone could provide some insight as to how to perform the statistical analysis on these data (i.e. test each dataset for normality and then compare them using ANOVA).
Thanks,
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Failing Normality Test
Thank you. Here is the example raw data and the data generated using the script.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Failing Normality Test
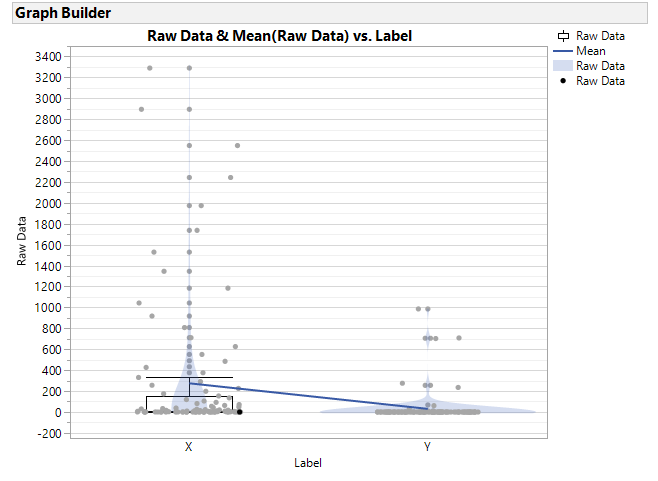
I would try graphing the data as well. Put the column shown in the Distribution on Y and what ever you are planning for the X in ANOVA on X in graph builder. If you notice the data clustering in both dimensions, then you do not have continous data and testing for normality does not make sense, nor does using ANOVA in Fit Model. It would be more likely that you would use Fit Model with a different distribution (using Generalized Linear Models) to perform your ANOVA.
Honestly it looks like the data is categorical and not continous. Kind of like a rating response.
Data Scientist, Life Sciences - Global Technical Enablement
JMP Statistical Discovery, LLC. - Denver, CO
Tel: +1-919-531-9927 ▪ Mobile: +1-303-378-7419 ▪ E-mail: chris.kirchberg@jmp.com
www.jmp.com
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Failing Normality Test
Thanks!
For the ANOVA portion I stacked the data and used the label for each data set as the X, with Y being each collection of numbers like the one I attached above. I was looking at the data a little more and Dunnett's Method looks promising, as the difference Matrix can tell me how different the datasets are. However, the R-squared listed under 'Summary of Fit' is still very low (0.002).
I also tried using Fit Model with a Generalized Linear Model personality, Poisson Distribution and Log link function but the Prob>ChiSq is still less than 0.05. Works the same if I use a Normal distribution.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Failing Normality Test
Hi All,
After doing some research on the topic I decided to calculate the Ranks of each dataset and perform the Fit Y by X using the Ranks (continuous) as the Y values and the labels (nominal) of each dataset as the X. Then I proceeded by perfoming a test of equal variances--since equal variances are necessary for all non-parametric tests. After establishing my variances are equal (the original data is not only not normal but also fails the test for equal variances), I performed a Kruskal-Wallis Test and finished off with both the Steel and Dunn Post Hoc tests. At this point I think the statistical approach makes sense and the conclusion of the tests are in line with real life observations.
Can anyone advice if the above methodology is the correct approach from the statistical point of view? And as final question, in terms of post hoc tests, what is considered to be standard practice by statisticians: Steel or Dunn? Both yield the same ranking and reach the same conclusion. I believe both correct for inflated Type I error when comparing pairs.
Thank you so much for all the input!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Failing Normality Test
@garibay90 , not sure about the tests you are running, I haven't read much if anythign about them.
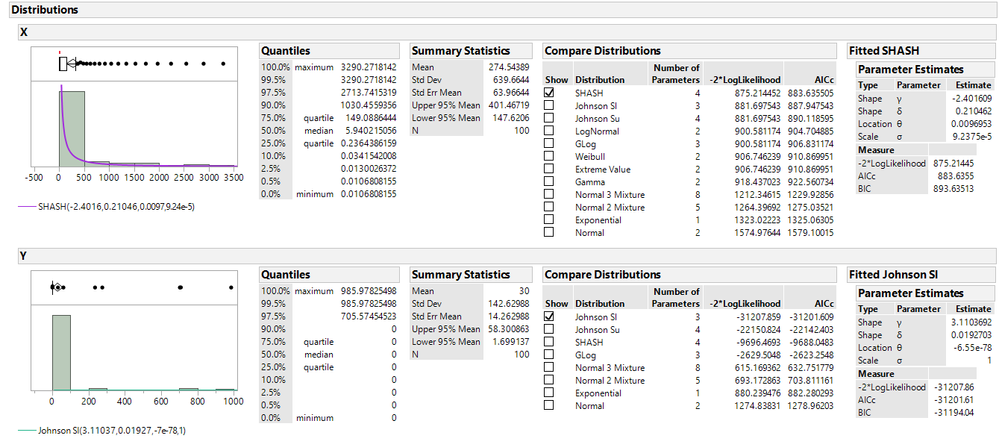
I tried fitting your "X" and "Y" columns of data using the Life Distribution Platform and the the best JMP could come up with there strictly on the basis of Liklihood, AICc and BIC is Lognormal, and Zero Inflated Weibull, respectively. Nether fit is good in my mind: use your eyes to look at the extent to which the points follow and non-linear coherent path on the transformed N-Q plots. If the points don't fall pretty close to the straight line and/or exhibit a curvature, then the transformation is not a very good fit.
Based on my understanding, if you want to run a 2-group comparison using a standard normal parametric statistical hypothesis test (such as ANOVA = t-test for the 2-sample case, then you would need to apply the same transformation to normality for both groups. And the data has to be reasonably normal after you've applied that transformation to both.
JMPs SHASH distribution may be a good fit for your "X" column, actually the best I could find (you can use Analyze Distribution > Fit All and JMP will generate a fit to this one for you). But it won't give you a good fit for your "Y" column. Actually in my experience, you will be very hard pressed to find any transformation which will validly fit this data. You have too many "0.0000" values in your dataset. I've dealt with this issue before and in the end you really have no choice but to run a non-parametric analysis. With data like "Y" I wouldn't trust the inferences I make from the non-parametric tests unless I was reasonably confident that the estimates I am trying to infer on are reasonably representative of the population from which the sample came. For example, if I am running a Wilcoxon test which looks at the score difference between groups, can I rust that the confidence interval of the score mean difference is really representative of the population mean difference? If I choose a test comparing the medians, do I have reason to think that the estimate of the median from my sample in "Y" and the corresponding confidence interval around the estimate, is representative of where the true estimate could be in the population?
I am not aware of a non-parametric test correction for extremely unequal variances. But I could be wrong. For the normal parametric tests, there is a standard correction for unequal variances, but the correction is based on an estimate and is not an exact solution. Look up the “behrens fisher problem” on Google.
If you go with the SHASH distribution to transform your data (which I don't think it works particularly well at all for your “Y” data), then you get evidence of equal variance between groups. You get evidence that there is a statistically significant difference between the means between groups, where the “Y” column mean is 0.62 units lower than the “X” column mean.
Just taking a step back here and looking at this groups, despite the fact that you have “unruly” data, its pretty clear to me that these groups are behaving numerically differently. You are getting a bunch of 0 values for “Y” but not for your “X” group.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Failing Normality Test
@PatrickGiuliano Thank you so much for taking the time to look at my data in so much detail. I checked and unfortunately I do not have the SHASH fit available--I'm working with JMP 10. However, I do agree that at this point a non-parametric approach for mean comparison is probably my best bet.
"For example, if I am running a Wilcoxon test which looks at the score difference between groups, can I rust that the confidence interval of the score mean difference is really representative of the population mean difference? If I choose a test comparing the medians, do I have reason to think that the estimate of the median from my sample in "Y" and the corresponding confidence interval around the estimate, is representative of where the true estimate could be in the population?" Good question, I am new to non-parametric tests so I'm not quite sure about this but as I understand it, what matters is the order of the ranks relative to each other and not so much the actual numerical value. If someone could clarify this that would be awesome.
The two columns behave differently because the raw data is a histogram, where X (Column 1) are the bins and Y (Column 2) are the counts in each bin. Hence the amount of "0.0000" values in the dataset.
Thank you so much for all your input!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Failing Normality Test
@Mark_Bailey @Chris_Kirchberg Would you guys be able to verify the methodology above listed makes sense and is in line with standard statistical practices? Thank you! P.S. I'm referring to my post above Patrick's.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Failing Normality Test
I may not endorse, verify, or validate a method used by someone else.
I think that you will generally receive helpful suggestions here but you must decide if the the advice is appropriate in your case.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Failing Normality Test
I understand. Thank you!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Failing Normality Test
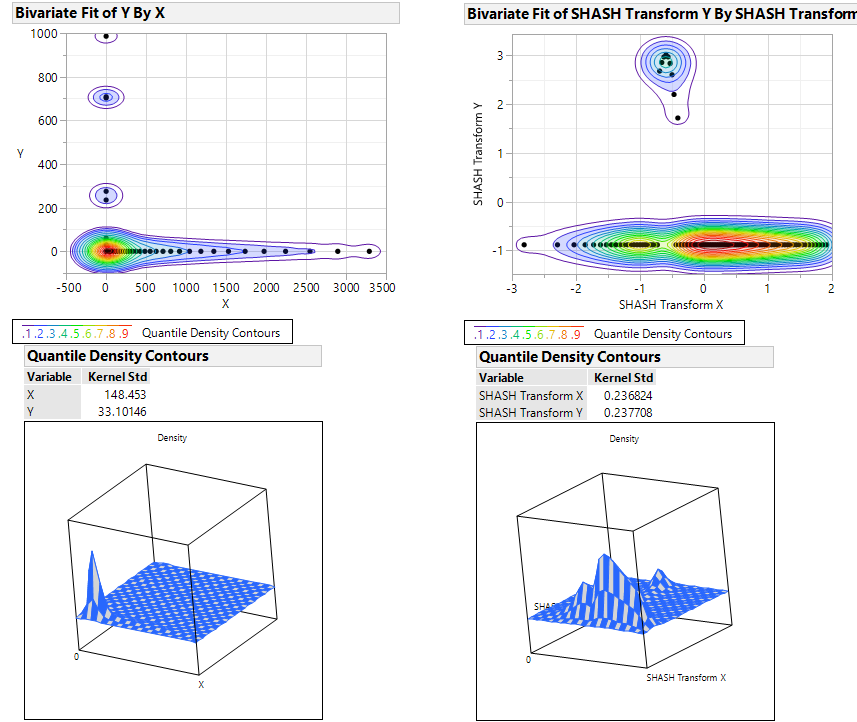
using @garibay90 's data, I used Fit Y by X instead of Graph Builder because the platform offers more options for coloring and changing the contour lines. Also discovered this "Mesh Plot" option which looks like a Bivariate Histogram.
- « Previous
-
- 1
- 2
- Next »
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us