- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Extreme Value Continuous Fit Documentation?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Extreme Value Continuous Fit Documentation?
I'm looking for some information on the "Extreme Value" distribution type, found in the Distribution Platform under Continuous Fit. Specifically, what is the formula for this cumulative distribution? Here's an example:
Names Default To Here(1);
dt = Open("$SAMPLE_DATA/Big Class.jmp");
Distribution(
Continuous Distribution(
Column(:height),
Quantiles(0),
Histogram(0),
Vertical(0),
Outlier Box Plot(0),
Normal Quantile Plot(1),
Fit Distribution(Extreme Value(Spec Limits(LSL(50), USL(70))))
)
);
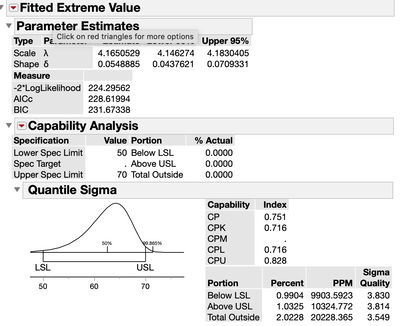
Here's a pic of the fit in the Distribution report. There are two parameters, lambda and delta.
I checked the "JSL Syntax Reference > JSL Functions > Probability Functions". The closest functions I can see are the "SEV Distribution" and "LEV Distribution", which both also take 2 parameters in addition to the independent variable x.
However, the values I get using either of these functions with the parameters in the Distribution report do not jibe. E.G: at my LSL of 50, the report says 0.9904% of the distrubution is below my lower limit. However:
x = 50; //my LSL
mu = 4.1650529; //taken from report
sigma = 0.0548885; //taken from report
pLEV = LEV Distribution(x, mu, sigma);
pSEV = SEV Distribution(x, mu, sigma);
Show(pLEV, pSEV);Both functions return a probability of 100%. In fact, they remain 100% unless I lower x to ~4. So clearly either these aren't the right functions or I'm missing something.
Any ideas?
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Extreme Value Continuous Fit Documentation?
See this part of the Help system: Continuous Fit Distributions.
You find the information yourself. Select Tools > Help and click on the Fitted Extreme Value outline in Distribution platform. It will take you to the Help for this model. The first page is an overview but it contains a link to the statistical details that you want.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Extreme Value Continuous Fit Documentation?
See this part of the Help system: Continuous Fit Distributions.
You find the information yourself. Select Tools > Help and click on the Fitted Extreme Value outline in Distribution platform. It will take you to the Help for this model. The first page is an overview but it contains a link to the statistical details that you want.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Extreme Value Continuous Fit Documentation?
Thanks Mark. That's the answer. For benefit of others, the necessary transforms are shown below:
x = 70; //my LSL
lambda = 4.1650529; //taken from report
delta = 0.0548885; //taken from report
alpha = Exp(lambda); //scale
beta = 1/delta; //shape
pex = Weibull Distribution(x, beta, alpha);
pex2 = 1-Exp(-(x/alpha)^beta); //taken from wiki as a confirmation
Show(pex, pex2);Sidenote: Interesting that when I clicked on "Continuous Fit Distributions" in the JMP Help Search Results, it just goes to a blank page. In case anyone has the same issue, try opening the page as a separate window. Might be my OS (Mac) or my browser (Safari).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Extreme Value Continuous Fit Documentation?
Glad this information helped.
BTW, I use Safari on Mac at home and I do not have this problem with the Help system.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us