Exploring data with ANCOVA

[#1]

Hello,

I have 3 independent variables, a continuous covariate (Mass), a categorical nominal variable (sex: M and F) and another categorical nominal variable (Site location: North, Middle, and South) and one dependent variable, continuous (mercury concentration). I am interested in testing the hypothesis " If the variation of mass and sex in an organism can be standardized (homogenized, accounted for, smoothed over), then that animal can reflect the bioavailability of mercury in the site of the North location, Middle location, and Southern location." 

I tried to explore the use of an ANCOVA, by including my covariate (mass) in my fit model analysis with the categorical variable (sex) and the other categorical variable (site location), as well as the interaction terms. My intention is by accounting for mass and sex within the model fit, I can build an interaction plot for the site locations to see if there is a difference in mercury concentration among them and report their LSmeans as they have been statistically adjusted as if the sexes within those locations had a standardized mass.

Y= mercury concentration

X Mass + Site location + sex + Mass*Sex + Mass*Site location

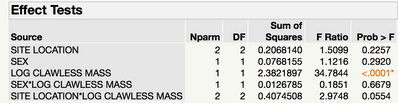
Interestingly, when this model is ran, this is what my effects test looks like

I want to validate that after I have accounted for the covariate as it covaries with sex mercury concentration and site location mercury concentration, we find that there are no statistical differences between the sexes and among the sites. 

I am curious if I am treating my independent variables correctly here given the hypothesis I want to test. Any and all assistance will be helpful 

[#2]

Sorry, I'm a bit confused by your terminology.  Covariates are typically associated with experimental design. The covariates are typically noise factors (factors that are impossible /difficult/costly to control). It does not appear you have an experimental design, but more likely a sampling plan where you have identified x's associated with the data collected, but I could be misinterpreting your situation.

If you had an experimental design, it appears you have 2 factors (sex and site location) and a covariate.  Is this correct?  The covariate is meant to be a random variable (measurable noise) which has a numeric value for each treatment.  The resulting model is a mixed model (fixed effects, factors manipulated at specified levels and the random variable). Usually you do not look for covariate by factor interactions in the model.  The covariate is typically noise (some uncontrollable variable) that you wish to assign and remove the effects of to increase the precision of detecting the manipulated factor effects.

There are a host of methods to analyze an existing data set to look for relationships between x's (mass, sex and location) and y's.

[#3]

That is the funny thing about hypotheses. They do not all come out the way we thought they would. (I bet Yogi Bera might have at least one quote to that effect.)

Assuming there are no data problems, I would reduce the model. One interaction appears to be important if not statistically significant at an arbitrary alpha = 0.05. Reduce the model one term at a time, starting with higher-order terms. I would remove SEX*MASS. The SS and p-values will change with the reduced model. I would next remove SEX unless it becomes important.

We assume the data are correct. Look for data problems using data plots alone and within the modeling platform.

We assume that the model is unbiased (no lack of fit), the estimates are reasonably uncorrelated, and the response variance is constant and normally distributed. The errors should be ~N( 0, sigma ). Use the residual plots that are provided to assess these assumptions.