- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Data Fitting - Urgent
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Data Fitting - Urgent
Hi,
I have a data table with various values.
I want to model the following data.
The Data set I have are T,U,V,W,X,Y,Z
The Equation I want to model is
Z^g = a*(T^h) + b*(U^i) + c*(V^j) + d*(W^k) + e*(X^m) + f*(Y^n)
Please need help urgently.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Data Fitting - Urgent
Open JMP and select Help > Books > Predictive and Specialized Modeling. Chapter 13 in the JMP 13 edition of this guide covers the Nonlinear platform in detail. It explains and demonstrates how to define a custom nonlinear model such as yours.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Data Fitting - Urgent
You can use the Nonlinear platform to fit any custom model including the one you've shown above.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Data Fitting - Urgent
Greetings, Jay!
As usual, Jeff is spot-on; The Nonlinear platform is the place to be for your model.
One potential problem you may face is that you will need to supply initial guesses for the values of the parameters in your model. Hopefully, the physical situation can suggest some starting values, or perhaps you have a previous analysis that could suggest some? If not, it's not too onerous to fit a number of models with ranges of parameter values and see which do the best, even though this approach is somewhat contrary to the classical philosophy of nonlinear modeling.
If you can share your data, or even some anonymized dataset, perhaps we can urgently help?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Data Fitting - Urgent
A linear solution was able to provide some insight into the problem but I would still like to know how to go about modelling the non-linear solution. I am attaching the dataset as requested...
Regards,
Jay
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Data Fitting - Urgent
Open JMP and select Help > Books > Predictive and Specialized Modeling. Chapter 13 in the JMP 13 edition of this guide covers the Nonlinear platform in detail. It explains and demonstrates how to define a custom nonlinear model such as yours.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Data Fitting - Urgent
Thank goodness you didn't really need help urgently! :) This definitely was not a quick turn-around!
The Nonlinear platform is a great workhorse, especially for mechanistic models, but it can be finicky and tempermental. As Leland Wilkinson has said "Nonlinear modeling is an art; multiparameter nonlinear modeling is rococo."
I don't really even understand what "problem" you're trying to solve, but I couldn't get the Nonlinear platform to converge your model reliably on your dataset. When it did converge, the model diagnostics were poor. I think it's because a) I was guessing semi-randomly at starting values for the parameters, b) the parameters are highly intercorrelated, and c) the data and model you provided are missing important variables that describe the actions of the response.
I explored your dataset with the Neural platform, but even it had poor description capabilities. That leads me to think that you are missing important independent variables in your data and model. Like maybe Neighborhood and Land Price...and interactions...and probably others...
'Sorry to be less-than-helpful, but JMP can't perform magic, even though it can often seem magical. I think you might need a better dataset and a better mechanistic model to achieve the results you seek.
Not really worth the wait, I imagine...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Data Fitting - Urgent
I think that setting up Nonlinear, as previously described, is straight-forward but the results may disappoint you.
- You have collinear predictor variables, so all model fitting procedures will have difficulty except PLS.
- The non-linear model that you specified will require careful attention to the starting values, as stated previously. Is there a theoretical basis for such a model?
- The non-linear model parameters will be highly correlated, as stated previously, which will further hamper fitting procedures.
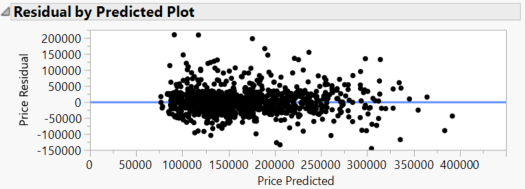
I tried fitting a linear model using ordinarly least squares regression based on a second-order polynomial function with second-order cross terms. I achieved a reasonably good fit after removing non-significant terms. This result shows no particular problem in the residual analysis except that there is a large component of random errors in the pricing.
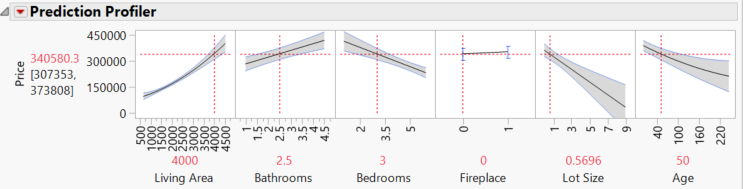
There is also apparently a noticeable right skew in the distribution of the residuals, so a GLM with non-Gaussian distribution might improve the fit. This fit has R square of 0.95, which is quite good. The effects of the predictors through this model seem reasonable, too, and quite interpretable:
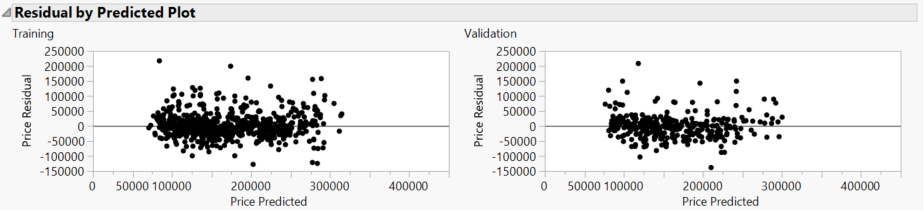
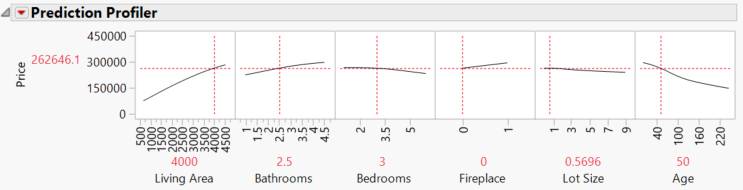
Interestingly, the Neural model using 4-6 hidden nodes gives similar results, which is encouraging:
The residuals show do particular problem.
The prediction profiles are quite similar except for Lot Size, but I did not spend a lot of time on my model selection using Fit Least Squares.
It seems to come down to which is more important, fitting a particular non-linear model or predicting. The former will be very difficult with results that are likely no better in performance than alternative models. The latter does not provide theoretical rigor but is likely to perform as well as can be expected.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us