- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- DOE: Significant model with significant lack-of-fit
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
DOE: Significant model with significant lack-of-fit
Hi all JMPers,
I'm facing an issue with a DOE and would like your opinion on that.
I'm trying to model two responses Y1,Y2 as a function of 2 factors X1,X2, their first order interaction and quadratic effects.
To do so, I have the data from a full 2^3 factorial design plus two replicate experiments (non-centered) from a previous dataset.
I have no issue with Y1 but when it comes to Y2, its appears that nor X1*X2 nor X2*X2 factors are significant.
When I re-run the script without these 2 factors I obtain the following:
My model is significant (p-value <0.0001), has a high R² (0.96) but also has a significant lack-of-fit (p-value 0.024) !
What should I do ? I cannot repeat the experiments and transform the response may be tricky here.
Do I have to throw my model to garbage ?
Thanks for the help.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: DOE: Significant model with significant lack-of-fit
Quentin: You ask: "Do I have to throw my model in the garbage?" Only if the model is, to paraphrase George Box, "not useful". LOF is just one, and I emphasize only one test that is used to evaluate model usefulness. Have you taken a look at your residual plots? Are they problematic from a prediction point of view? How about the magnitude of the size of residuals across the experimental space? I don't get too hung up on LOF especially if I've exhausted the means to modify the model by adding terms. What I'd do is take a look at the predictions vs. residuals...and evaluate the what I call 'magnitude of the miss' or the residual value. Is the size or direction of the residual problematic from a practical point of view? If not...why worry about LOF?
Lastly I'd encourage you to run some additional trials for model verification purposes. This step should be done regardless of LOF results anyways to verify model utility...if these verification runs turn out OK from a practical point of view...again, who cares about LOF?
Good luck.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: DOE: Significant model with significant lack-of-fit
Quentin: You ask: "Do I have to throw my model in the garbage?" Only if the model is, to paraphrase George Box, "not useful". LOF is just one, and I emphasize only one test that is used to evaluate model usefulness. Have you taken a look at your residual plots? Are they problematic from a prediction point of view? How about the magnitude of the size of residuals across the experimental space? I don't get too hung up on LOF especially if I've exhausted the means to modify the model by adding terms. What I'd do is take a look at the predictions vs. residuals...and evaluate the what I call 'magnitude of the miss' or the residual value. Is the size or direction of the residual problematic from a practical point of view? If not...why worry about LOF?
Lastly I'd encourage you to run some additional trials for model verification purposes. This step should be done regardless of LOF results anyways to verify model utility...if these verification runs turn out OK from a practical point of view...again, who cares about LOF?
Good luck.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: DOE: Significant model with significant lack-of-fit
Thank you Peter.
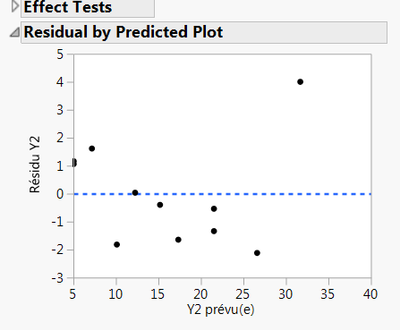
I already looked to the residuals (see graph below). There is no observable latent pattern in the residuals plot, but there is a random dispersion of the residuals. The Y2 response vary between 0 and 100 (it's a yield), so I consider that the magnitude (<5%) of the residuals is acceptable. However, I may say that the residual corresponding to the higher Y2 value is 'relatively' higher (~4) that the others suggesting a lower degree of confidence for the prediction of the high Y2 values. This was also visible when plotting Y2 observed vs. Y2 predicted with confidence intervals.
So do you think with all these observations taken into account I could reasonably accept this model and try to validate it with additional runs ?
Thanks again for the help!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: DOE: Significant model with significant lack-of-fit
Quentin: Bill Worley offers some great advice that, quite frankly, I'm embarrassed I didn't suggest as well. I was just too focused on your worrying about a p value associated with the LOF test to even consider the issues Bill raises. All too often I think some folks try to distill the 'accept and use the model' decision to one and only one model diagnostic statistic. I call this behavior falling victim to 'mononumerosis'.
On to your last question in the post: "So do you think with all these observations taken into account I could reasonably accept this model and try to validate it with additional runs ?"
It would be highly presumptuous of me to make a recommendation one way or the other to you regarding '...accept this model..'. From afar I'm reluctant knowing little about your problem, the conduct of the experiment, knowledge of the process, etc. to begin to give you anything other than a very uninformed opinion. Hence I'll decline.
This much I will offer; During my tenure as a industrial statistician over decades, I can't tell you how many times I'd be asked this very same question. My reply was always something like this: "OK Quentin, rather than give you my opinion, here's what I suggest you do. Pause for a moment and think about the decision the data, the experiment, and your analysis are leading you towards. Think about the consequences of that decision from a practical point of view. Especially if the outcome is less than desirable. How do you feel about that decision? Not from a statistical point of view but from a practical point of view. Now, in the pit of your stomach, how do you feel about that decision? If you feel some butterflies...then stop, pause, and circle back for more information/data/analysis/experimentation/conjecture...whatever it is...but delay the decision."
A long time ago I read a quote by Moen, Nolan and Provost that went something like this: "In the final analysis it's not a question of statistical inference but a question of a degree of belief." Or as Dr. Deming was known to say, "The most important figures are unknown and unknowable." P - values we know...but the most important 'figures' are unknowable.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: DOE: Significant model with significant lack-of-fit
Quentin,
I am going to pile on to Peter's answer.
You state that you pulled two samples from a previous data set and added them to your DOE results. It is very likely that you will bias the outcome of your DOE/model by using those "outside" samples to build your model.
Just a suggestion, take those two samples out and refit your models. Then use those samples as test data by adding them to your data table and see where the predictions comes out. Make sure to save your prediction formula to the data table first and then add the "new" data at the bottom. Compare the actual data with the predicted values. You can also do this with your prediction profiler by changing the input settings and seeing what the predicted value is on the left.
As for your residuals plot, it looks like the point in the upper right is a potential outlier and this will also bias your results. Refit the model without that point and then check your fit model parameters.
Hope this helps,
Bill
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: DOE: Significant model with significant lack-of-fit
Many thanks to Bill and Peter for these advices.
Taking out the 2 samples and use them for validation works well and the predicted results are very closed to the actual ones.
However there is a small change in the model for Y1. Previously, all the linear, quadratic and interaction effects of X1 and X2 were significant for Y1 (p-value<0.05).
However, now that I took the 2 additional samples out, the X2 factors has a non significant effect on Y1 (p-value=0.0852) whereas all the other factors are significant as before.
My question is: I cannot remove X2 without removing its quadratic and interaction effects with X1, which are both significant, so can I keep X2 in my model stating that it is significant at the 0.1 confidence level ?
I believe that the approach suggested by Bill is better that the one I use but before using it I just want to make sure that now the model for Y1 is also valid.
Thank you for your answers.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: DOE: Significant model with significant lack-of-fit
Quentin,
You can keep X2 because of the effect heredity with interaction terms. Said another way, you have interactions with X2 that are significant so therefore you can keep that main effect (X2) in your model. With JMP 12. you could use the Effects Summary capability in fit model to remove terms and only remove the X2 to see how it changes your model, but in your case I would recommend just keeping it in the model.
Bill
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us