- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Custom design factor constraints
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Custom design factor constraints
bonjour,
Je réalise un DOE contenant 2 réponses (A et B) et 2 facteurs (C et D). Les deux facteurs sont des concentrations disons de 5 à 9 pour C et de 10 à 25 pour D. Je souhaite réaliser un plan avec comme contraintes sur les facteurs, le fait que le rapport D/C doit être égal ou supérieur à 4. Comment dois-je réaliser cela. De plus, quelles types de facteurs dois-je encodé ? continu ou discret ? je suis un peu perdu.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Custom design factor constraints
Hello @SeanCor,
Bienvenue dans la Communauté JMP !
Pour mieux comprendre comment gérer des contraintes dans la création de DoE avec JMP, je vous conseille la lecture de l'article de blog de @Jed_Campbell : Demystifying Factor Constraints - JMP User Community
Concernant vos questions, quelques réponses, questions et remarques :
- Si les concentrations des facteurs C et D peuvent varier de façon continue, alors il s'agit très vraisemblablement de facteurs continus. Les facteurs de type "discret" ne peuvent prendre que quelques valeurs ordonnées définies sur l'ensemble de la fourchette possible. Plus d'infos sur les types de facteurs ici : Factors (jmp.com)
- Quel est votre objectif avec ce plan ? Etudier les effets de ces deux facteurs de manière quantitative ? Avoir un modèle prédictif ? Souhaitez-vous analyser une possible interaction ou des effets quadratiques de ces facteurs ? Ces questions ne sont qu'un point de départ, mais vous permettront de mieux cerner quel type de plan est le plus adapté, et faire de bonnes décisions sur la construction et l'analyse du plan.
- Concernant votre contrainte relationnel entre C et D, vous pouvez l'ajouter dans plusieurs plateformes de construction de plan. J'ai pris l'exemple ici avec la plateforme Custom Design :
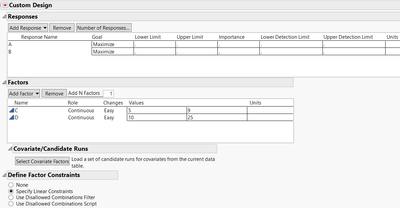
- Entrer vos réponses, facteurs et ranges :
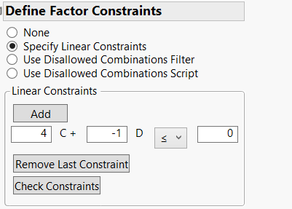
- Dans la partie "Define Factor Constraints", cliquer sur "Specify Linear Constraints". Comme vous souhaitez que le ratio D/C soit supérieur ou égal à 4, une remise en forme de cette équation donne :
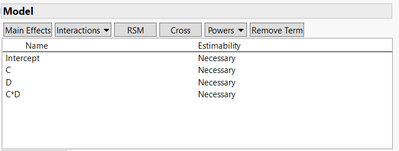
Vous pouvez donc entrer cette contrainte dans la partie dédiée :4 * :C + -1 * :D <= 0 - Définissez le type d'effets que vous souhaitez estimer grâce à votre plan. Dans l'exemple ici, j'ai ajouté l'interaction entre C et D, les effets principaux de C et D ainsi que l'intercept sont entrés par défaut :
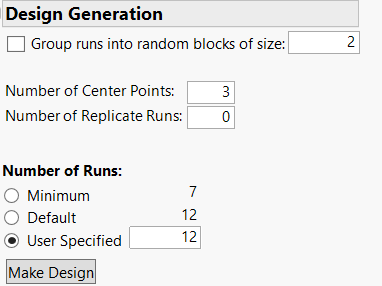
- Vous pouvez ensuite définir un nombre de réplicats, de points centraux, et vous avez également une certaine flexibilité sur le nombre de runs à réaliser, puis vous pouvez lancer la génération du plan "Make Design". Dans cet exemple, j'ai choisi 3 points centraux pour pouvoir évaluer si un effet quadratique est éventuellement présent et vérifier l'ajustement du modèle avec un test de Lack-Of-Fit, pour un nombre de runs recommandé égal à 12 :
- Entrer vos réponses, facteurs et ranges :
A noter que dû à cette contrainte relationnelle, vos facteurs C et D ne sont plus indépendants. Estimer les effets individuels de chacun risque d'être plus difficile.
Il est important de bien distinguer si cette contrainte relationnelle est physiquement nécessaire pour réaliser les expériences (auquel cas elle doit être prise en compte dans le plan pour éviter de générer des expériences physiquement impossibles à réaliser ou dangereuses), ou si c'est une contrainte "préférentielle", où vous pensez avoir de bons résultats. Dans le second cas, mieux vaut enlever cette contrainte pour éviter tout biais au départ et avoir une vue sur votre espace expérimental la plus neutre et complète possible. Pour comprendre où, comment et pourquoi vous avez des résultats positifs dans votre espace expérimental, vous avez besoin de disposer également de résultats négatifs.
Finalement se pose également la question de savoir si les concentrations individuelles de vos facteurs constituent les informations d'intérêt, ou si c'est plutôt le ratio qui semble avoir un intérêt. Dans le second cas, vous pourriez combiner les facteurs C et D en un facteur (ratio), que vous feriez évoluer sur une certaine plage, et qui ne nécessiterait pas de plan d'expériences.
Voici le script utilisé pour la génération du plan d'expériences avec contrainte mentionné ici :
DOE(
Custom Design,
{Add Response( Maximize, "A", ., ., . ), Add Response( Maximize, "B", ., ., . ),
Add Factor( Continuous, 5, 9, "C", 0 ), Add Factor( Continuous, 10, 25, "D", 0 ),
Set Random Seed( 1047040825 ), Number of Starts( 55959 ),
Add Constraint( [4 -1 0] ), Add Term( {1, 0} ), Add Term( {1, 1} ),
Add Term( {2, 1} ), Add Term( {1, 1}, {2, 1} ), Center Points( 3 ),
Set Sample Size( 12 ), Optimality Criterion( "Make A-Optimal Design" ),
"A-Optimality Parameter Weights"n( [1 1 1 1] ), Simulate Responses( 0 ),
Save X Matrix( 0 ), Make Design, Set Run Order( Randomize ), Make Table}
);
Vous trouverez également en PJ le plan généré pour illustration de cette réponse (avec ajout dans la table d'une colonne calculée D/C pour que vous puissiez vérifier que toutes les expériences générées de cette méthode respectent votre contrainte).
En espérant que cette réponse vous aide,
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Custom design factor constraints
Hello @SeanCor,
Bienvenue dans la Communauté JMP !
Pour mieux comprendre comment gérer des contraintes dans la création de DoE avec JMP, je vous conseille la lecture de l'article de blog de @Jed_Campbell : Demystifying Factor Constraints - JMP User Community
Concernant vos questions, quelques réponses, questions et remarques :
- Si les concentrations des facteurs C et D peuvent varier de façon continue, alors il s'agit très vraisemblablement de facteurs continus. Les facteurs de type "discret" ne peuvent prendre que quelques valeurs ordonnées définies sur l'ensemble de la fourchette possible. Plus d'infos sur les types de facteurs ici : Factors (jmp.com)
- Quel est votre objectif avec ce plan ? Etudier les effets de ces deux facteurs de manière quantitative ? Avoir un modèle prédictif ? Souhaitez-vous analyser une possible interaction ou des effets quadratiques de ces facteurs ? Ces questions ne sont qu'un point de départ, mais vous permettront de mieux cerner quel type de plan est le plus adapté, et faire de bonnes décisions sur la construction et l'analyse du plan.
- Concernant votre contrainte relationnel entre C et D, vous pouvez l'ajouter dans plusieurs plateformes de construction de plan. J'ai pris l'exemple ici avec la plateforme Custom Design :
- Entrer vos réponses, facteurs et ranges :
- Dans la partie "Define Factor Constraints", cliquer sur "Specify Linear Constraints". Comme vous souhaitez que le ratio D/C soit supérieur ou égal à 4, une remise en forme de cette équation donne :
Vous pouvez donc entrer cette contrainte dans la partie dédiée :4 * :C + -1 * :D <= 0 - Définissez le type d'effets que vous souhaitez estimer grâce à votre plan. Dans l'exemple ici, j'ai ajouté l'interaction entre C et D, les effets principaux de C et D ainsi que l'intercept sont entrés par défaut :
- Vous pouvez ensuite définir un nombre de réplicats, de points centraux, et vous avez également une certaine flexibilité sur le nombre de runs à réaliser, puis vous pouvez lancer la génération du plan "Make Design". Dans cet exemple, j'ai choisi 3 points centraux pour pouvoir évaluer si un effet quadratique est éventuellement présent et vérifier l'ajustement du modèle avec un test de Lack-Of-Fit, pour un nombre de runs recommandé égal à 12 :
- Entrer vos réponses, facteurs et ranges :
A noter que dû à cette contrainte relationnelle, vos facteurs C et D ne sont plus indépendants. Estimer les effets individuels de chacun risque d'être plus difficile.
Il est important de bien distinguer si cette contrainte relationnelle est physiquement nécessaire pour réaliser les expériences (auquel cas elle doit être prise en compte dans le plan pour éviter de générer des expériences physiquement impossibles à réaliser ou dangereuses), ou si c'est une contrainte "préférentielle", où vous pensez avoir de bons résultats. Dans le second cas, mieux vaut enlever cette contrainte pour éviter tout biais au départ et avoir une vue sur votre espace expérimental la plus neutre et complète possible. Pour comprendre où, comment et pourquoi vous avez des résultats positifs dans votre espace expérimental, vous avez besoin de disposer également de résultats négatifs.
Finalement se pose également la question de savoir si les concentrations individuelles de vos facteurs constituent les informations d'intérêt, ou si c'est plutôt le ratio qui semble avoir un intérêt. Dans le second cas, vous pourriez combiner les facteurs C et D en un facteur (ratio), que vous feriez évoluer sur une certaine plage, et qui ne nécessiterait pas de plan d'expériences.
Voici le script utilisé pour la génération du plan d'expériences avec contrainte mentionné ici :
DOE(
Custom Design,
{Add Response( Maximize, "A", ., ., . ), Add Response( Maximize, "B", ., ., . ),
Add Factor( Continuous, 5, 9, "C", 0 ), Add Factor( Continuous, 10, 25, "D", 0 ),
Set Random Seed( 1047040825 ), Number of Starts( 55959 ),
Add Constraint( [4 -1 0] ), Add Term( {1, 0} ), Add Term( {1, 1} ),
Add Term( {2, 1} ), Add Term( {1, 1}, {2, 1} ), Center Points( 3 ),
Set Sample Size( 12 ), Optimality Criterion( "Make A-Optimal Design" ),
"A-Optimality Parameter Weights"n( [1 1 1 1] ), Simulate Responses( 0 ),
Save X Matrix( 0 ), Make Design, Set Run Order( Randomize ), Make Table}
);
Vous trouverez également en PJ le plan généré pour illustration de cette réponse (avec ajout dans la table d'une colonne calculée D/C pour que vous puissiez vérifier que toutes les expériences générées de cette méthode respectent votre contrainte).
En espérant que cette réponse vous aide,
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Custom design factor constraints
Bonjour,
Merci énormément pour cette réponse qui m'aide beaucoup. Il s'agit en effet de la réalisation d'un modèle à but prédictif d'output à partir d'input afin d'offrir des packages, c'est à dire différentes possibilités en fonction des envies. Admettons que A soit un rendement en concentration et B un pourcentage. Je souhaite prédire en fonction des différentes concentrations des facteurs C et D les réponses A et B. Cependant, la réalisation du modèle comme vous me le décrivez abouti à des concentration à virgule très précises et difficile à réaliser en pratique. De plus la contrainte demande au ratio d'être égal ou supérieur à 4 et nous avons uniquement des ratios allant de 4 à 4,91, pas plus, est ce normal ?
je vous remercie
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Custom design factor constraints
Hello @SeanCor,
Concernant les valeurs des facteurs très précises, c'est une conséquence de l'algorithme utilisé pour créer le plan optimal. Voir les réponses à ce sujet :
Solved: Re: How are odd factor settings in D-optimal RSM generated - JMP User Community
Solved: Re: Random decimals incorporated in mixture screening design - JMP User Community
Concernant la contrainte de ratio, cette dernière est très exigeante : si vous prenez les valeurs extrêmes de D et C (max pour D, min pour C), vous arrivez à un ratio maximum égal à 25/5 = 5. Donc il est normal de retrouver des ratios compris entre 4 et 5. Est-ce que cette contrainte de ratio peut être modifiée, ou les fourchettes des facteurs agrandies (plus faibles valeurs pour C, plus grandes valeurs pour D) pour obtenir une plus grande fourchette de ratio ?
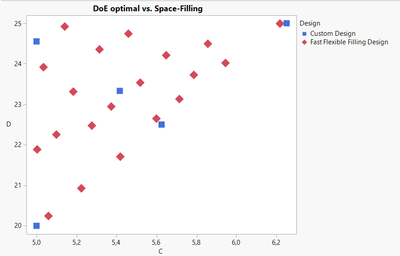
Concernant votre objectif de prédiction, un plan type Space-Filling est peut-être plus approprié, car permettant de répartir les points dans votre espace expérimental et permettant une grande flexibilité dans la modélisation (notamment avec des algorithmes de Machine Learning) et le nombre de points requis (pas de minimum, mais il faut choisir un nombre de points raisonnable).
Vous pouvez le construire dans la plateforme Space-Filling dispo dans "DoE", "Special Purpose", "Space-Filling" :
Vous trouverez en PJ un exemple de plan Space-Filling construit avec 20 expériences avec vos facteurs, réponses et la contrainte de ratio.
Une comparaison de la répartition des points dans l'espace expérimental selon le type de plan choisi :
En espérant que ce complément de réponse vous aide,
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us