- JMP will suspend normal business operations for our Winter Holiday beginning on Wednesday, Dec. 24, 2025, at 5:00 p.m. ET (2:00 p.m. ET for JMP Accounts Receivable).
Regular business hours will resume at 9:00 a.m. EST on Friday, Jan. 2, 2026. - We’re retiring the File Exchange at the end of this year. The JMP Marketplace is now your destination for add-ins and extensions.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Custom DOE: constraints for factors depending eachther
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Custom DOE: constraints for factors depending eachther
Hi, i´m desining a DOE with factors with conditions depending each other.
e.g.:
1) for every run, the sum of X1/X2/X3 should be 8000
or
2) mean of X1/X2/X3 should not exceed X4
How can i put such constraints to my DOE?
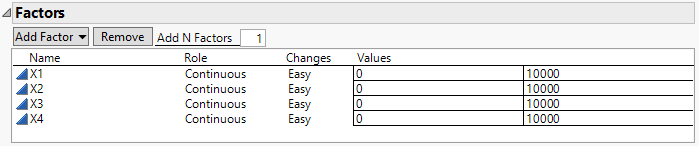
| X1 | continous | 0 | 10000 |
| X2 | continous | 0 | 10000 |
X3 | continous | 0 | 10000 |
Many thanks in advance!
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Custom DOE: constraints for factors depending eachther
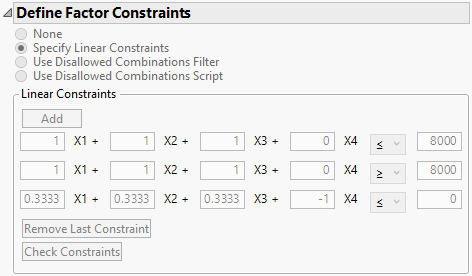
Your first constraint is inconsistent and it creates a singularity in the design. First of all, none of the first three factors can exceed 8,000, so an upper limit of 10,000 does not make sense. Secondly, you only have 2 independent factors. The third factor is completely determined by the sum of the first two factors. So you could design the experiment with just the first two factors and then use a column formula to determine the setting of the third factor in order to make a run or you can design the experiment with all three factors but remove the third from any model.
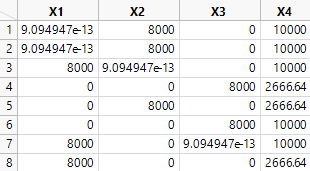
Here are my results by way of an example.
The upper bounds are not realistic for your experiment.
Here is the definition of the constraints that I used.
Together with the model containing only the intercept and main effects, I get this design with warnings.
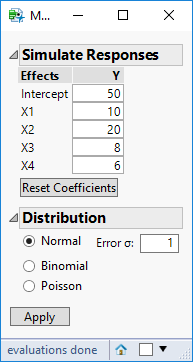
The very small values can be replaced by zero. I simulated the data to show the analysis.
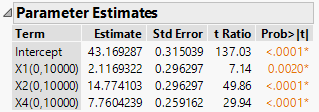
I begin the analysis as usual but I remove any terms with X3. Here is the result.
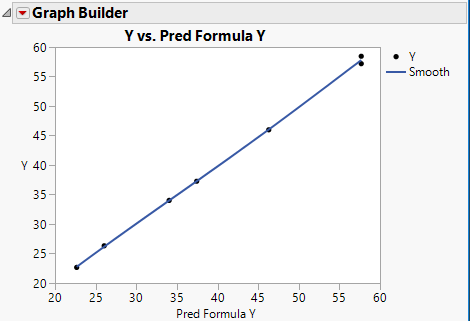
Note that these estimates won't match the simulation because they used coded factor levels. The model does, though, predict very well.
Another approach that might work is to treat this experiment as a mixture design. That approach will require you to rescale your factors as 0 to 1 or 0.8. Then change the mixture sum to 0.8. You would only enter X1 and X2, not X3, in this approach. You would only need one constraint for the X4 requirement with a modification to cover that X3 is no longer explicitly in the design.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Custom DOE: constraints for factors depending eachther
Your first constraint is inconsistent and it creates a singularity in the design. First of all, none of the first three factors can exceed 8,000, so an upper limit of 10,000 does not make sense. Secondly, you only have 2 independent factors. The third factor is completely determined by the sum of the first two factors. So you could design the experiment with just the first two factors and then use a column formula to determine the setting of the third factor in order to make a run or you can design the experiment with all three factors but remove the third from any model.
Here are my results by way of an example.
The upper bounds are not realistic for your experiment.
Here is the definition of the constraints that I used.
Together with the model containing only the intercept and main effects, I get this design with warnings.
The very small values can be replaced by zero. I simulated the data to show the analysis.
I begin the analysis as usual but I remove any terms with X3. Here is the result.
Note that these estimates won't match the simulation because they used coded factor levels. The model does, though, predict very well.
Another approach that might work is to treat this experiment as a mixture design. That approach will require you to rescale your factors as 0 to 1 or 0.8. Then change the mixture sum to 0.8. You would only enter X1 and X2, not X3, in this approach. You would only need one constraint for the X4 requirement with a modification to cover that X3 is no longer explicitly in the design.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Custom DOE: constraints for factors depending eachther
Mark Bailey has outlined a good approach. Just a little bit more on the mixture approach that he mentioned at the end.
You do not have to rescale your X1 to X3 for that approach. You can tell JMP that your mixture sum is 8000 rather than the default of 1. That option is available under the red triangle pop-up menu in the custom DOE dialog.
If you do take the mixture approach, remember that your model fitting results will be different as you will now be fitting a Scheffe Mixture model rather than a standard regression model.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Custom DOE: constraints for factors depending eachther
Thank you very much for the tip using sum of the mixture! I applied it to my DOE.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Custom DOE: constraints for factors depending eachther
Thank you very much for the detailed solution!
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us