- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Crow-AMSAA Confidence Intervals - Delta Method
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Crow-AMSAA Confidence Intervals - Delta Method
Hello,
I am using JMP 16.2.0 to calculate Reliability Growth and am trying to understand the math behind the profiler confidence intervals on the Crow AMSAA models. The help article states that: "The delta method is applied to this expression to obtain an estimate of its variance. This estimate is used to construct a 95% Wald-based confidence interval. The resulting confidence limits are then transformed using the exponential function to give confidence limits for the estimated cumulative number of events at time t." I have not been able to find an example of utilizing the delta method that I can follow. Is there a way to on JMP to look at the formula/math that goes into these calculations?
Thank you!
-John
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Crow-AMSAA Confidence Intervals - Delta Method
At the moment, JMP does not produce a formula in JSL that a user can directly reproduces the results.
The mathematical details are available in statistical analysis books. My reference is Statistical Methods for Reliability Data . Section C.7.4 and C.7.7 in that book are what you need.
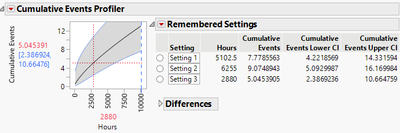
The needed results, however, are available in the report, especially the profilers in the report; see this screenshot:
Based on your description, seems that you would like to get a table which lists desired confidence intervals. I suggest looking into the "Remember Settings" feature in the profiler: https://www.jmp.com/support/help/en/17.1/#page/jmp/prediction-profiler-options.shtml
Following is a screenshot of remembered settings, which record confidence intervals at three different time points.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Crow-AMSAA Confidence Intervals - Delta Method
The formula/math of the delta method can be found here: https://en.wikipedia.org/wiki/Delta_method
The method can be applied well if the result of g(.) function is approximately normal.
For any g(.) function in hands, the above may not be true. Sometimes a transformation on g(.) function is necessary, e.g. h(.).
For such a situation, apply the delta method on h(g(.)) first, then use the inverse of h(.) to get desired results of g(.).
In other words, get intervals of h(g(.)), say h_Low and h_High, using delta method on h(g(.)), then use h^(-1)(h_Low) and h^(-1)(h_High) to get the intervals for g(.), where h^(-1) is the inverse of h(.).
In above JMP documentation, log function is the h(.).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Crow-AMSAA Confidence Intervals - Delta Method
Thank you for this information but I admit I am still lost. I am uncertain what the resulting formula of the delta method applied to the h(.) should give me. I am attempting to recreate confidence intervals for numerous time inputs simultaneously, so I would love to be able to input my parameters and times of interest in a table and have a JMP formula to create these confidence bands.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Crow-AMSAA Confidence Intervals - Delta Method
At the moment, JMP does not produce a formula in JSL that a user can directly reproduces the results.
The mathematical details are available in statistical analysis books. My reference is Statistical Methods for Reliability Data . Section C.7.4 and C.7.7 in that book are what you need.
The needed results, however, are available in the report, especially the profilers in the report; see this screenshot:
Based on your description, seems that you would like to get a table which lists desired confidence intervals. I suggest looking into the "Remember Settings" feature in the profiler: https://www.jmp.com/support/help/en/17.1/#page/jmp/prediction-profiler-options.shtml
Following is a screenshot of remembered settings, which record confidence intervals at three different time points.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us