Criteria of distribution fit to select within the Process Capability option

[#1]

I use the Analyze/Quality and Process/Process Capability and after selecting the "Y, Process" data and "By" selection, I then select under "Distribution Options", I select Distribution "Best fit".

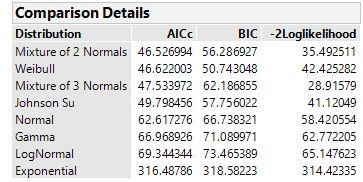
This then fits numerous data distributions to my data set and recommends the highest AICc BIC -2Loglike

Comparison Details

My question is there any recognized rationales to select AICc over BIC or over -2Loglike (any reference articles or experiences) and how close do these values have to be to one another for them to be considered similar. For example the above first 4 distributions are about the same given they are c.46 to 50, but am I right saying the Normal should not be used as its alot larger being c.63, how close can they be to be considered similar and dissimilar?? (again any references or experiences would be appreciated).

Regards Ian

[#2]

These criteria are based on information theory. The -2L is a measure of model bias, so the smaller this value, the less bias in model. We generally want the model with minimal bias. Without regard to model variance, you just increase the complexity of the model (e.g., add more terms to the linear model) until you have a perfect fit. That result is fine if you only want to model the current data set. Such a model does not 'generalize' to represent new data, though. So the -2L provides information about the model but is generally regarded as poor criterion for model selection.

AIC and BIC are both based on -2L plus a penalty for the variance. The minimum AIC or BIC trades off bias and variance optimally. The difference between the two criteria is in the definition of the penalty. The penalty in both cases is a function of the model complexity and the sample size. AIC is generally favored over BIC but some types of models seem to be selected better with BIC depending on the interpretation of complexity.

The difference between the two models with the best AIC can be helpful when assessing the candidate models. An AIC difference less than 4 indicates that the second best model has significant support from the data, a difference of 4 to 10 indicates considerably less support, and a difference greater than 10 indicates essentially no support.

NOTE: these criteria are dependent on the training data.

It is best when the choice of the model also includes available knowledge about the observed system. How do the data occur? Can that information guide the choice of the model? Model selection should not be just about fitting data.

[#3]

Thanks Mark for this, so for the 4 distributions
#1) Mixture of 2 Normals
#2) Weibull
#3) Mixture of 3 Normals
#4) Johnson Su

These all have similar AICc, but are within a range of 4 and are considered similar, the other distributions from "Normal" onwards is greater that 10 AICc points and therefore should not be considered.

Yor statement "An AIC difference less than 4 indicates that the second best model has significant support from the data", so you recommend #2 Weibull is the best option, why is this chosen is it that "Mixture" distributions are demoted in preference against the more classic Weibull and the like distributions (eg Normal, Gamma etc).

Apreciate your help in this, is there any literature that descibes this ?

Cheers Ian

[#4 · Accepted solution]

No. Using AICc alone, the mixture of two normal distributions is the best model and the Weibull distribution is the second best model of those models fit to the same data. Because the Weibull model's associated AICc is close to that of the normal mixture model, we can say that it, too, has much support from the data.

If I had other, independent reasons for choosing the Weibull distribution (e.g., historical preference, theory of the process, et cetera), then that information along with the AICc might lead me to chose it over the normal mixture model.

A good reference is Kenneth P. Burnham and David R. Anderson (2002) "Model Selection and Multimodel Inference: A Practical Information-Theoretic Approach, Second Edition," Springer.