- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Creating a prediction interval with monte carlo simulation
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Creating a prediction interval with monte carlo simulation
Hi,
I was wondering if anyone could help me.
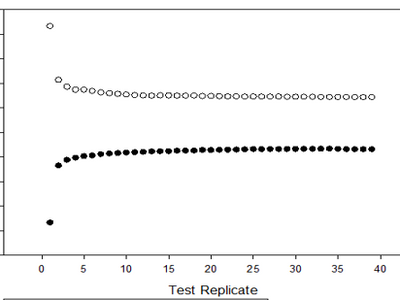
I have a set of data in two columns. Column one contains a Run ID while Column 2 contains data generated by the run. My end goal is to plot the 95% prediction interval of the confidence intervals produced by N, N-1, N-2, N-3... until you only have two datapoints per Run, where N = initial number of replicates. Therefore step by step, If for example I had 40 replicates per run, I would like for JMP to randomly select 39 replicates for each run, conduct a lower 95% and upper 95% confidence interval for each Run, then conduct a lower 95% Prediction interval for the lower 95% confidence intervals of each run and a upper 95% prediction interval for the upper 95% confidence intervals of each run. This would get repeated with 38 replicates, 37 replicates... until there is only 2 replicates. I would like to graph on the x-axis the replicate number and plot both the upper 95% Preidiction interval and lower 95% prediction interval similar to what is shown below:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Creating a prediction interval with monte carlo simulation
Hi,
I believe I have an answer for you. It makes use of the Bootstrapping functionality in JMP Pro, and for that reason will only work with JMP Pro. Please take a look and let me know if it does what you are after.
Names Default To Here( 1 );
dt = Open( "$SAMPLE_DATA/Big Class.jmp" );
dist=dt<<Distribution(Y(:Weight));//Create Distribution report of column "Weight""
//JMP PRO REQUIRED FOR NEXT STEP
boot_dt=(dist << Report)[TableBox( 2 )] << Bootstrap(
40,
Fractional Weights( 1 ),
Split Selected Column( 1 )
);//Bootstrap 40 samples of Summary Statistics
boot_dist=boot_dt[2]<<Distribution(Y(Column(3)));//Create Distribution of Bootstrap samples for whichever statistic ends up in Column 3 - "Lower 95% Mean"" in our case.
lowCL = {};//container for lower confidence limits
upCL = {};//container for upper confidence limits
nsims = {}; //container for number of simulations - for x-axis of GB report
lowCL[1] = Report( boot_dist )["Bootstrap Confidence Limits"][Number Col Box( 2 )][1];//lower a=0.05 limit
upCL[1] = Report( boot_dist )["Bootstrap Confidence Limits"][Number Col Box( 3 )][1];//upper a=0.05 limit
boot_dist << Close Window;
nsims[1] = N Rows( boot_dt[2] ) - 1;//Estimates were taken using all rows of table, except the first.
// dist << Close Window;
For( i = 2, i <= N Rows( boot_dt[2] ) - 2, i++, //Create distribution reports after excluding rows one-at-a-time, save values in lowCL, upCL and nsims containers.
boot_dt[2] << Select Where( Row() == i );
boot_dt[2] << Exclude;
boot_dist=boot_dt[2]<<Distribution(Y(Column(3)));
lowCL[i] = Report( boot_dist )["Bootstrap Confidence Limits"][Number Col Box( 2 )][1];//lower a=0.05 limit
upCL[i] = Report( boot_dist )["Bootstrap Confidence Limits"][Number Col Box( 3 )][1];//upper a=0.05 limit
boot_dist << Close Window;
nsims[i] = N Rows( boot_dt[2]) - i;
);//end of For-loop, containers now have values for each row.
graphdt = New Table(); //create new table to generate GB report
lowCLcolumn = graphdt << New Column( "Lower Confidence limit" ); //column of lower confidence limits
graphdt << add Rows( N Items( lowCL ) ); //add rows
lowCLcolumn << Set Values( lowCL ); // set values from lowCL into column
upCLcolumn = graphdt << New Column( "Upper Confidence limit" ); //column of upper confidence limits
upCLcolumn << Set Values( upCL );//set values from upCL into column
Nsimscol = graphdt << New Column( "N" ); //column of number of rows in simulated estimates table that were not exlcuded (x-axis of GB report)
Nsimscol << Set Values( nsims ); // set values from nsims into column
//create GB report
gb = graphdt << Graph Builder(
Size( 531, 456 ),
Show Control Panel( 0 ),
Variables( X( :N ), Y( :Lower Confidence limit ), Y( :Upper Confidence limit, Position( 1 ) ) ),
Elements( Line( X, Y( 1 ), Y( 2 ), Legend( 7 ) ) )
);- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Creating a prediction interval with monte carlo simulation
By the way, this solution makes use of bits of a script from an add-in presented at the JMP Discovery Summit Europe 2020.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us