Confidence intervals for difference in proportions

[#1]

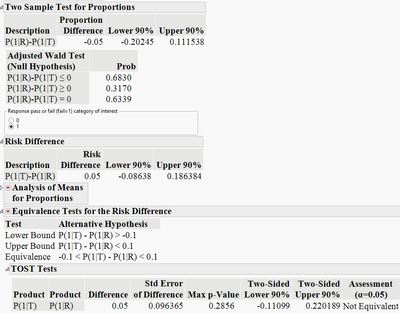
Hi All: I've attached an example data set to highlight an issue that confuses me.  Suppose I want a confidence interval for the difference in two proportions.  Should be easy enough. So, via Fit Y by X (JMP v18.0.0), I get three intervals under the following headings:

Two Sample Test for Proportions.

Risk Difference

TOST Tests

As you can see, the intervals are not consistent with each other.

My question(s) is this:

1. Why are they not the same?

2. What formulae is used for each?

3. Am I missing something?

I did find this for the Two Sample Proportions Report (could be more explicit IMHO).

 Two Sample Test for Proportions Report

Thanks for your learned consideration!

[#2 · Accepted solution]

FYI, I queried tech support and received the following.

The three tests use slightly different methods, which results in the difference you are observing in the confidence intervals.  The methods are all described in the SAS documentation here:  https://go.documentation.sas.com/doc/en/statcdc/14.2/statug/statug_freq_details53.htm#statug.freq.fr...

1. For the Two Sample Test for Proportions JMP is using the Agresti-Caffo limit: Script follows.

x1 = 19; n1 = 20;
x2 = 18; n2 = 20;

/* proportion difference */
diff = x1/n1 - x2/n2;

/* Calculation for CI for Two Sample Test for Proportion */
p1 = (x1+1)/(n1+2);
p2 = (x2+1)/(n2+2);
pdiff= p1 - p2;
lower = pdiff - normalquantile(.95)*sqrt(p1*(1-p1)/(n1+2)+p2*(1-p2)/(n2+2));
upper = pdiff + normalquantile(.95)*sqrt(p1*(1-p1)/(n1+2)+p2*(1-p2)/(n2+2));

show(lower, upper);

2. The Confidence interval for Risk Difference uses the Wald interval: Script follows.

/* Calculation for CI for Risk Difference */
p1 = (x1)/(n1);
p2 = (x2)/(n2);
diff = x1/n1 - x2/n2;
lower = diff - normalquantile(.95)*sqrt(p1*(1-p1)/(n1)+p2*(1-p2)/(n2));
upper = diff + normalquantile(.95)*sqrt(p1*(1-p1)/(n1)+p2*(1-p2)/(n2));

show(lower, upper);

3. The confidence limits for the risk difference in equivalence test uses the Miettinen-Nurminen (score) confidence limits: Script follows.

/*  Calculation for CI for Equivalence Test */

/* mnStdEquivDiff is a function to calculate the standard deviation of se(p1-p2) */

mnStdEquivDiff=Function({n11, n21, n1, n2, n, margin },
{default local},

p1_hat=n11/n1;
p2_hat=n21/n2;

theta=n2/n1;

d=-p1_hat*margin*(1+margin);
c=margin^2+margin*(2*p1_hat+theta+1) + p1_hat + theta*p2_hat;
b=-(1+theta+p1_hat + theta*p2_hat + margin*(theta+2));
a=1+theta;

v=b^3/(3*a)^3-b*c/(6*a^2) + d/(2*a);
if(v>0, sign=1, sign=-1);

u=sign*root(b^2/(3*a)^2 -c/(3*a));
w=(pi()+ArcCosine(v/u^3))/3;

p1_tlt=2*u*cosine(w)-b/(3*a);
p2_tlt =p1_tlt -margin;

var1=p1_tlt*(1-p1_tlt)/n1;
var2=p2_tlt*(1-p2_tlt)/n2;

correct=n/(n-1);
correct=1;

std_diff=root(correct*(var1+var2));
std_diff;
);


/* Calculation using the example data */
n11=19;
n21=18;

n1=20;
n2=20;
n=40;
alpha=0.05;

p1=n11/n1;
p2=n21/n2;
diff=p1-p2;
show(diff);

maxit=100;
conv = .00000001;

z=ChiSquare Quantile( 0.9, 1 );
pdiff = diff; 
correct=1;

//calculate the lower confidence limit
inc=1+diff;
converged = 0;
for (i = 0, i < maxit, i++, 
	inc *= 0.5;
	lcl = pdiff - inc;
	var = mnStdEquivDiff(n11, n21, n1, n2, n, lcl); 
	var = var * var;
	var *= correct;

	d = diff - lcl;
	
	if( var > 0, score=(d * d) / var,  score=. );
	
	if (score < z, pdiff = lcl);

	if ((inc < conv) | abs(z - score) < conv,  
		converged = 1;
		break();
	);
);

if ((i == maxit) & converged==0, lcl = MACMISSING);


//calculate the upper confidence limit
inc=1-diff;
converged = 0;
for (i = 0, i < maxit, i++, 
	inc *= 0.5;
	ucl = pdiff + inc;
	var = mnStdEquivDiff(n11, n21, n1, n2, n, ucl); 
	var = var * var;
	var *= correct;

	d = diff - ucl;
	
	if( var > 0, score=(d * d) / var,  score=. );
	
	if (score < z, pdiff = ucl);

	if (   (inc < conv) | abs(z - score) < conv,  
		converged = 1;
		break();
	);
);

if ((i == maxit) & converged==0, ucl = MACMISSING);

show(lcl, ucl);

They also said they would: "open two requests with the development team. One for the documentation team, to add the references (and statistical details) for each of the different methods. For the other I will add a feature request to the development team to allow user to choose the desired method."

As usual, tech support is very helpful, thorough, and professional.