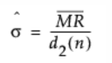Computing std devs for Control Charts?

[#1]

Hi.  I have a question for any 6-sigma folks out there.  In the Quality and Process Methods section of the User Manual, under "Statistical Details for Control Chart Builder", the standard deviation seems to be approximated using the range.   For example, for XmR charts, the standard dev formula is:

where MR-bar is the average of the moving range and d2 is a value from a lookup table.

I'm not unfamiliar with this methodology for computing sigma and have seen it used in several other process control references. My question, though, is why?  That is, why do we approximate it using this method, when we could instead simply use the traditional formula for computing sigma:

I understand that technically, any computation of sigma is an estimate of the "true" value, so perhaps one might argue that one formula is as good as another.  However, the latter formula comes from the actual definition of standard deviation.  I also understand there's the question of biased vs unbiased and the Bessel correction factor (N-1), but I feel the same issue would apply to both formulas, yes?  Lastly, I understand that the latter formula requires more computation steps.  Computation speed might have been an issue many decades ago, but that doesn't seem like and especially valid reason anymore.

Perhaps I'm wrong about one or more of my assumptions above, but if so, I'd love to know why.  I've searched around the internet and other references, and I've never been able to come up with a satisfactory answer.  Does anyone know?

Thanks, and Happy New Year!

[#2]

Here are the reasons for using the R-bar/d2 method:

1. First and foremost, it requires you plot the data (i.e., range, MR charts) to determine if the sample is consistent and stable BEFORE calculating any statistic.  This is a great idea in just about every situation.

2. The range will actually converge on the "true" population standard deviation faster than with the long form for small sample sizes.

3. The second most important concept is the ranges are from RATIONAL subgroups and represent the variation due to the X's changing within subgroup.  Therefore this estimate of variation is assignable to potential sources of variation.  Extremely important if you are trying to understand causal structure.  When you use the formula, the variation is pooled across all sources of variation.

[#3]

Thanks statman.  Please see my responses below:

1. I don't disagree that plotting the data is an important part of determining consistency.  But I think you would agree that there's nothing inherent about either mathematical calculation of standard deviation that requires a plot.  Similarly, there is nothing about either method that prevents one from plotting the data.  In this regard, I see no advantage of one over the other.

2.  Having an optimal convergence to the "true" value would definitely be an advantage.  But I've not seen this mentioned before and would like to understand the underlying principle better.  Is there any source that explains this a little better?

3. I may not be grasping this point fully.  Could you elaborate some more?  My question is regarding the method for computing std dev in general, not necessarily computing std dev for subgroups for comparison purposes.

Thanks again.

[#4]

To your first point, you are "required" to plot the data to assess consistency. You wouldn't use R-bar/d2 if the range displayed inconsistency (out-of-control on a control chart).  There is no "requirement" for any consistency check before the mathematical computation.  You asked about computing enumerative statistics for control charts.  I assume you want to use control charts as they were intended (BTW, this has nothing to do with six sigma).

I suggest you read:

Shewhart, Walter A. (1931) “Economic Control of Quality of Manufactured Product”, D. Van Nostrand Co., NY

“The engineer who is successful in dividing his data initially into rational subgroups based on rational theories is therefore inherently better off in the long run”  Shewhart

It is good that you reached out to Don as he has an exceptional grasp of the concepts elaborated by Shewhart.

Regarding your third point, the question is what are you doing with the data?  As you suggest, we are always estimating enumerative statistics.  How good does your estimate need to be?  Do you really need the estimate to be "right" to use control charts?  My point is regarding the appropriate use of control chart method (as elaborated by Shewhart).  First, is the basis for comparison consistent and stable (are the within subgroup sources of variation acting consistently/commonly)?  This is assessed with range charts.  Second, which sources of variation have greater leverage on the responses of interest, the within or between?  This is the question answered with the X-bar chart.

“Analysis of variance, t-test, confidence intervals, and other statistical techniques taught in the books, however interesting, are inappropriate because they provide no basis for prediction and because they bury the information contained in the order of production. Most if not all computer packages for analysis of data, as they are called, provide flagrant examples of inefficiency.”

Deming, W. Edwards (1975), On Probability As a Basis For Action. The American Statistician, 29(4), 1975, p. 146-152

I'm not sure if your questions are curiosity or if you have run into situations where one method is superior to another and has had an impact on understanding the problems you face.  I have had the opportunity to use multiple methods thousands of times in real life situations with real data and found there to be little consequence in which method you use to estimate the standard deviation.  To be honest, I don't actually care which one gives a better estimate as having the right value doesn't make understanding causality any better.  I am more concerned with finding the causal relationships that affect variation (and the mean) than reporting the estimate.

[#5]

Replying to my own comment.  I wanted to supply more info the problem.

1. I'm currently reading EMP III by Donald Wheeler, where several statistics such as Mean, Std Dev, Median are computed from the average moving range, similar to what I describe above.  I've actually reached out directly to him with this same question, so hopefully he will get back to me soon.  In the meantime, I wanted to ask the JMP community.  

2. I've also reviewed few similar posts regarding this question.  

A:  https://community.jmp.com/t5/Discussions/IR-Control-charts-limits/m-p/249674/highlight/true#M49029

This response indicates there are multiple methods of computing std deviation.  But I would disagree.  There's multiple methods to approximate standard deviation, but I would argue that the traditional formula for standard deviation is well defined (second formula in my original post).  This comes from the definition of the second moment of a distribution.  I.e. the standard deviation has that formula because that's how it was defined.

B: https://community.jmp.com/t5/Discussions/Control-Chart-3-Sigma/m-p/11356/highlight/true#M10885

This response is basically that the range-based formula was used for computational ease originally and is still used for historical reasons.  I would argue that if a more correct method is available and feasible, the sub-optimal approximation should no longer be used.

C: https://community.jmp.com/t5/Discussions/Control-Chart-3-Sigma/m-p/11357/highlight/true#M10886

This response from the same thread suggests that the range-based method is dependent on the ordering of the data, where the traditional method is not.  I'm not sure how that is an argument for using the range-based method.  If anything, I would argue that this shows why the range-based method should not be used, as your computations should not depend on the subjectivity of how the data is ordered.

3.  This is a problem for me because it leads to ambiguity in the results.   That is, unless the user is aware that this alternate approximative method is being used, they will compute something different and wonder why their results are off.  On multiple occasions I've had users approach me and confidently assert that "JMP is computing standard deviation incorrectly".  These folks are now Matlab and Excel for their analyses instead of JMP bc they think it's broken.  At best, it will be an uphill battle to win them back over to JMP.

Hope that provides a little more explanation & rationale behind my question.  As always, thanks for the help.

[#6]

Again, your query was regarding computations for control charts. For 2C, I suggest you understand the difference between enumerative and analytical problems.  

Deming, W. E. “Foundation for management of quality in the Western World”. Paper presented at the meeting of Management Sciences, Osaka, Japan. (1989, October; revised 1990, April).

Deming, W. E., “On probability as a basis for action,” The American Statistician, 29(4), 1975, p. 146-152.

Time order (or some rational order) is imperative for analytical problems.

Regarding your third point, have you actually tried looking at any data sets you have and comparing how much different the estimates are?  What do you mean by "their results are off"?  Off of what?  I assure you that JMP is more than capable of calculating statistics with precision and accuracy.  Comparing JMP to Excel or Minitab for that matter and deciding which to use based on these estimates is, IMHO, ridiculous.

If you are interested in a more technical comparison of estimates of variation using ranges (this has nothing to do with control charts), see here:

Patnaik, P. B. “The Use of Mean Range as an Estimator of Variance in Statistical Tests.” Biometrika, vol. 37, no. 1/2, 1950, pp. 78–87. JSTOR, https://doi.org/10.2307/2332149.

[#7]

Hi statman.  Thanks for the replies.  Replying here to both: 

To your first point, you are "required" to plot the data to assess consistency.

There is no disagreement here.  I 100% agree with you that consistency must be confirmed.  Again, my point is that neither method prevents one from plotting the data to assess consistency.  Therefore, this requirement can not be used as an argument that one should or must use the range-based method instead of the traditional method for computing std dev.  

I assume you want to use control charts as they were intended (BTW, this has nothing to do with six sigma).

Although I think this is tangential to my question, I must disagree with your statement here.  The Six-Sigma process relies on control charts extensively.  This is where I was first introduced to the notion of approximating std dev using the range-based method.  Sadly, the rationale was not explained very well there either.  At the time I just shrugged my shoulders and moved on, but now I'm more curious.

Regarding your third point, the question is what are you doing with the data? [etc...]

The first thing that comes to mind is "Should the end goal of how I'm using this data matter?"  I can still see no reason why we should accept alternative approximative methods for a term such as std dev that has (IMO) already been well-defined and can be easily computed.  That is unless, there is a clear advantage to using the approximation method over the actual formula.  You did aim in that direction when you mentioned earlier that the approximation tends toward the "true" value more rapidly.  I would still like to understand that proof though. 

Time order (or some rational order) is imperative for analytical problems.

This is interesting.  If we assume a memoryless, Markov process, then the probability of one measurement is entirely independent of any previous measurement.  Therefore, the likelihood that a sequential set of measurements alternates between high, low, high, low... is the same as the likelihood a set of measurements will appear ordered from low to high.  In the former case, the average 2-pt moving range will be maximized.  In the latter, it will be minimized.  Both cases are equally likely, and yet they could provide drastically different computations of the std dev using the range-based method.  Are we ok with this?  Again, I would argue this is clear reason why the range-based method should not be used.  Using a methodology that would vary despite all the data points having the same value, just ordered differently, is still very puzzling to me.

Regarding your third point, have you actually tried looking at any data sets you have and comparing how much different the estimates are?  What do you mean by "their results are off"?  Off of what?  I assure you that JMP is more than capable of calculating statistics with precision and accuracy.  Comparing JMP to Excel or Minitab for that matter and deciding which to use based on these estimates is, IMHO, ridiculous.

You might be mistaking my colleague's comments as my own.  They are the one's who need to be convinced that JMP is the right platform, not me.  I'm just coming here to get the ammunition I need to do this.  At the same time, I do feel their questions/concerns are legitimate and would like to help them understand.

Patnaik, P. B. “The Use of Mean Range as an Estimator of Variance in Statistical Tests.” Biometrika, vol. 37, no. 1/2, 1950, pp. 78–87. JSTOR, https://doi.org/10.2307/2332149.

Thanks.  Will definitely have a look at this ref.

[#8]

Sorry, I tried to give you a response to your questions.  I am finding it difficult to make my points to you and based on your responses, you misinterpret them.  Of course, it could also be I misunderstand you...LOL.  In any case, I apologize if my responses aren't useful.  And I am extremely biased.

I will say control chart method was invented decades before six sigma (invented by Shewhart). 

Happy new year.

[#9]

No apology needed statman.  I appreciate your willingness to help explain these things to others.

Since my last post, I've finally come around.  I now agree that the range-based method of approximating std dev is the correct method for this case.  This website was helpful: https://r-bar.net/xmr-limits-moving-range/.  I'll do my best to explain the reasoning in my own words below.  For reference, here again are the two equations being discussed:

Sample Std Deviation (aka traditional method): 

Range-based approximation of std dev (specifically, the average of the 2-pt moving range, divided by d2):

Variability in a process can have multiple sources.  There's always some background noise, but there's also a possibility of the process shifting (i.e. inconsistency) which will add to the variability.  The usage of the 2 methods depends on the end goal.

The Sample Std Deviation incorporates all of these sources into its result.  If one wants to assess the overall dispersion of the data, this is the correct method.  

On the other hand, the Range-based method minimizes the contribution of sudden process shifts.  This is due to the nature of the average of the 2-pt moving range.  Process shifts can still impact the resulting value, but not nearly as much as they would the Sample std Deviation.  If one wants to assess the inconsistency of the data (as you would when using a control chart), this is the correct method.  

It may seem counterintuitive that one would want to assess inconsistency by using a method that minimizes the effect of inconsistency, but this is because we're using this value to establish the control limits needed to check for inconsistency.  The plots below might help (taken from https://r-bar.net/xmr-limits-moving-range/

On the left, there are no process shifts.  Here, both methods produce nearly the same standard deviation, and hence nearly the same control limits (= mean +/- 3*std dev).  On the right, there are 4 process shifts.  The control limits produced by the Sample Std Deviation (green lines) incorporate these shifts along with all the other variability, and consequently, they are much wider than the limits produced by the Moving Range method (red lines).  This is because the latter method minimizes the contribution of sudden process shifts.  It is because these contributions are minimized that the range-based std dev should be used to determine control limits.  Note that if the Sample Std Deviation were used to compute the control limits (green lines), one would conclude that the data is consistent.  However, inspection of the data shows it is clearly not.

In summary, not only should the Range-Based approximation be used for determining control chart limits, but the Sample Std Deviation should specifically not be used.  Otherwise, you may incorrectly conclude your data is consistent.

Afterthought 1:

I feel much of this confusion was caused by using the term "std deviation" and the symbols "s" and "σ" for both the Sample Std Deviation as well as the Range-Based approximation.  Although the values for latter can be very close to the former, they are not exactly the same, and as shown above, can sometimes differ greatly.  Plus, they do not serve the exact same purpose.  The former is for quantifying overall dispersion, while the latter is for assessing data consistency.  It would be nice if the Range-Based approximation of the std deviation were just named differently to help avoid confusion.  Perhaps "Ranged Dispersion" or "δ_r" (delta subscript r).

Afterthought 2:

I retract my point in my previous reply about the Range-Based method depending on the subjective ordering of the data, and therefore should not be used.  I realize now that the time-ordering of the data contains valuable information about the process too.  When the Sample Std Deviation is used, that information is ignored.  But that information is the key to understanding the process consistency.

Happy New Year everyone.

[#10]

OK, I'll try one more time specifically addressing your comments.

There is no disagreement here.  I 100% agree with you that consistency must be confirmed.  Again, my point is that neither method prevents one from plotting the data to assess consistency.  Therefore, this requirement can not be used as an argument that one should or must use the range-based method instead of the traditional method for computing std dev.

What data are you plotting for the SD equation?  What rational subgroups do you have? To get a range, you have to subgroup (even a MR has a subgroup of consecutive measures, though MR charts are not very useful for components of variation studies).  The rational subgroups (Mandatory element of control chart method) provide a way to separate and assign different sources of variation.  They provide the practitioner with a quantitative means to prioritize where they need to focus the next iteration of their study (which component has greater leverage).

Although I think this is tangential to my question, I must disagree with your statement here.  The Six-Sigma process relies on control charts extensively.  This is where I was first introduced to the notion of approximating std dev using the range-based method.  Sadly, the rationale was not explained very well there either.  At the time I just shrugged my shoulders and moved on, but now I'm more curious.

You miss my point.  Control chart methodology was invented long before Six Sigma came along.  It is unfortunate you did not have an instructor that could explain the reasons better (apparently I am having trouble as well).  Control charts are an analytical tool (as originally intended, not enumerative).  They are used to help understand causality.  We really don't care about how exact the numbers are compared to the true population statistics.  We want to approximate efficiently to understand how and why the numbers vary.  Knowing if the number is exactly correct doesn't help for analytical problems. (see the Deming quote I already posted...and perhaps read his paper I referenced)

The first thing that comes to mind is "Should the end goal of how I'm using this data matter?"  I can still see no reason why we should accept alternative approximative methods for a term such as std dev that has (IMO) already been well-defined and can be easily computed.  That is unless, there is a clear advantage to using the approximation method over the actual formula.  You did aim in that direction when you mentioned earlier that the approximation tends toward the "true" value more rapidly.  I would still like to understand that proof though. 

“Data have no meaning in themselves; they are meaningful only in relation to a conceptual model of the phenomenon studied”

Box, G.E.P., Hunter, Bill, Hunter, Stu “Statistics for Experimenters” So, YES, the purpose of the study does dictate how the data should be acquired.

What exactly do you mean by "the actual formula"?  You must realize this is also an approximation.  Ranges are quite efficient estimates when using control chart method.  Again we don't need to know the exact number. we want an efficient means of assigning where is the leverage in our investigation.

This is interesting.  If we assume a memoryless, Markov process, then the probability of one measurement is entirely independent of any previous measurement.  Therefore, the likelihood that a sequential set of measurements alternates between high, low, high, low... is the same as the likelihood a set of measurements will appear ordered from low to high.  In the former case, the average 2-pt moving range will be maximized.  In the latter, it will be minimized.  Both cases are equally likely, and yet they could provide drastically different computations of the std dev using the range-based method.  Are we ok with this?  Again, I would argue this is clear reason why the range-based method should not be used.  Using a methodology that would vary despite all the data points having the same value, just ordered differently, is still very puzzling to me.

MR charts are not very useful for components of variation studies.  They are used when there is NO rational subgroup (which, of course, is necessary for control chart method). Over time all of the x's will change within subgroup, so there really is no within and between leverage question to be answered.  MR charts are useful for assessing stability, though there is some likelihood of autocorrelation  They can be used on relatively small data sets (like when you are at the top of a nested sampling plan).  Again, in analytical problems we don't care about accuracy as much as precision. Your situation is completely theoretical.  Do you have any actual data sets where you have found one method to be superior than another?  Have you actually taken data sets from problems you've worked on and compared how each estimate would affect conclusions from your studies?  This would be worthy of discussion and debate.

"What does this situation mean in plain English? Simply this: such criteria, if they exist, cannot be shown to exist by any theorizing alone, no matter how well equipped the theorist is in respect to probability or statistical theory. We see in this situation the long recognised dividing line between theory and practice… the fact that the criterion we happen to use has a fine ancestry of highbrow statistical theorems does not justify its use. Such justifications must come from empirical evidence that it works. As the practical engineer might say, the proof of the pudding is in the eating" 

Shewhart, Walter A. (1931) “Economic Control of Quality of Manufactured Product”, D. Van Nostrand Co., NY

You might be mistaking my colleague's comments as my own.  They are the one's who need to be convinced that JMP is the right platform, not me.  I'm just coming here to get the ammunition I need to do this.  At the same time, I do feel their questions/concerns are legitimate and would like to help them understand.

You wrote the comments, I have no idea of the context.  I am conversant in all three software programs, though my bias is to use JMP.  If you want to convince users of the advantages of JMP over Minitab or Excel, there are several papers I suggest you read (you can google as well as me).  

For example https://statanalytica.com/blog/jmp-vs-minitab/ (simply the first one that showed up)

The argument over which program to use for estimates of enumerative statistics is not useful.  I have been successful convincing many Minitab users of the advantages of JMP in real world problems (better graphical displays of data...graph builder, ease of pattern recognition...color or mark by column, selecting a data point in one chart highlights it is every chart, REML, etc.).  Unfortunately, in reality, the folks that make the decisions regarding which to use as a corporation are folks that have no idea how to use statistics or the software.