Combinations of a list put into columns

[#1]

I'm trying to take a list of things and make all possible pairs of combinations appear in a set of two columns.  I currently have a script generated that does permutations (plus repeates of the same value in col a vs col b) but I'm struggling on how to reduce it down to combinations. For example, if the list of things was 1, 2, 3, 4, 5 then I don't need both 1/2 and 2/1, or 1/1.  Below is my script I currently have and I think I'm close, I just need a bit more to get where I need to be. I just need to make this script strictly do the choose 2 combinations of an arbitrary list. This particular example is using 5 things for simplicity.  thanks

Names Default To Here( 1 );

New Table( "Test",
	Add Rows( 5 ),
	New Column( "API 10", Numeric, "Continuous", Format( "Best", 15 ), Set Values( [4238939261, 4238939263, 4238939262, 4238939328, 4238939329] ) ),

);

Test = Data Table( "Test" );
APIs = Test:API 10 << get values;
working = New Table( "TestAPIComb", New Column( "API10" ), New Column( "API102" ), add rows( N Items( APIs ) ^ 2 ) );
APIs2 = Test:API 10 << get values;

theRow = 0;
	
For( APICNT = 1, APICNT <= N Items( APIs ), APICNT++,
	For( API2CNT = 1, API2CNT <= N Items( APIs2 ), API2CNT++,
		theRow++;
		:API10[theRow] = APIs[APICNT];
		:API102[theRow] = APIs[API2CNT];
	)
);	

[#2]

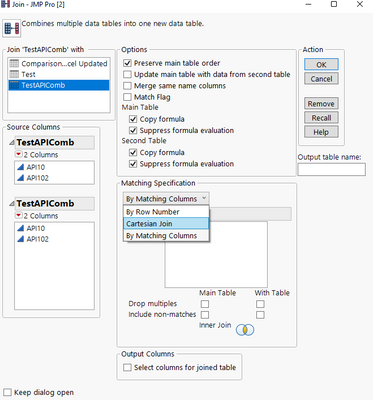
I have added a few lines of code that will eliminate the duplicate combinations.  In addition, I would suggest that you look into 

     Tables=>Join

at the Cartesian join capability. 

It produces the all possible combinations much faster than JSL code can do it.

Names Default To Here( 1 );

New Table( "Test",
	Add Rows( 5 ),
	New Column( "API 10", Numeric, "Continuous", Format( "Best", 15 ), Set Values( [4238939261, 4238939263, 4238939262, 4238939328, 4238939329] ) ),

);

Test = Data Table( "Test" );
APIs = Test:API 10 << get values;
working = New Table( "TestAPIComb", New Column( "API10" ), New Column( "API102" ), add rows( N Items( APIs ) ^ 2 ) );
APIs2 = Test:API 10 << get values;

theRow = 0;
	
For( APICNT = 1, APICNT <= N Items( APIs ), APICNT++,
	For( API2CNT = 1, API2CNT <= N Items( APIs2 ), API2CNT++,
		theRow++;
		:API10[theRow] = APIs[APICNT];
		:API102[theRow] = APIs[API2CNT];
	)
);	

dt = Data Table( "TestAPIcomb" );

// Arange data so order is the same for all rows
For( i = 1, i <= N Rows( dt ), i++,
	If( :API102[i] > :API10[i],
		hold = :API10[i];
		:API10[i] = :API102[i];
		:API102[i] = hold;
	)
);

// Find the duplicates
dt << Select Duplicate Rows( :API10, :API102 );

// Delete the duplicates
dt << delete rows;

[#3]

Most likely there are quite many ways of doing this (the cartesian join @txnelson is good starting point). Here is one option using just matrix calculations:

Names Default To Here(1);

// input list
m = [4238939261, 4238939263, 4238939262, 4238939328, 4238939329];
n_items = N Items(m);

// combination count
comb_count = Summation(i = 1, n_items - 1, i++);

m = Sort Ascending(m);

first_col = [];
second_col = [];
For(i = 2, i <= n_items, i++,
	first_col ||= Repeat(m[i - 1], n_items - i + 1)`;
	second_col ||= m[Index(i, n_items)]`;
);

dt = New Table("Combinations",
	Add Rows(comb_count),
	New Column("FirstCol", Numeric, Continuous, Values(first_col)),
	New Column("SecondCol", Numeric, Continuous, Values(second_col)),
);

[#4]

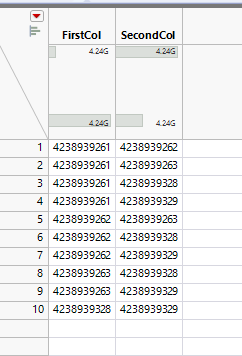
Thanks. I looked at what @txnelson suggested and also implemented the cartesian join and it returned 15 results instead of 10. I then just added a simple select condition at the end where if the first column = the second column then I also deleted them. Do either of you know which method is faster in JMP? i'm working with a large dataset and I'll try that matrix method as well but just didn't know if either of you know what should be more efficient. 

[#5]

I don't know which method would work fastest.  My suggestion is to run both of them and see which is fastest.

[#6]

Hi @jthi, any ideas if the initial list is string instead of number? Since matrix only works for number data type. 

[#7]

Without much changes you could just use initial list as numbers and then create conversion table to join character values based on those numeric values.

[#8]

Hello,

The NChooseK Matrix( ) function is tailor-made for problems like this. It is also reasonably quick, and especially useful for k>2. Check out the code below for an example of 2 things, and 5 things, chosen from a set of 26.

Cheers,

Brady

names default to here(1);

lis = words("abcdefghijklmnopqrstuvwxyz","");

// original example: choose 2
dt = astable( nchoosekMatrix(nitems(lis), 2), << column names({"x", "y"}) );
dt << new column ("first", character, << set values ( lis[dt:x << get values]));
dt << new column ("second", character, << set values ( lis[dt:y << get values]));
dt << delete columns (1::2);

// a more interesting example: choose 5
dt = astable( nchoosekMatrix(nitems(lis), 5), << column names( words("x1,x2,x3,x4,x5",",") ) );
for each ({ i }, 1::5, //i = 1;
	eval (substitute( expr(dt << new column ( "y"||char(i), character, <<set values ( lis[_EX_ << get values]  ) ) ), 
								expr(_EX_), 
								parse(evalinsert("dt:x^i^"))
	));
);
dt << delete columns (1::5);

[#9]

As to performance.

The code below generates the almost 2 million row table of pairs from a set of 2000 in a little under 6 seconds, which is a bit less than half as long as looping took. I don't know whether such performance is suitable for your purposes. Hopefully it is a feasible option for you.

Names Default To Here( 1 );

letters = Words( "abcdefghijklmnopqrstuvwxyz", "" );

// create a large list of random strings of length 10. use an AA to remove (unlikely) duplicates
lis = Associative Array( Repeat( {Concat Items( letters[J( 10, 1, Random Integer( 26 ) )], "" )}, 2e3 ) ) << get keys;

t1 = HP Time();

// looping solution
dt = new table( "xx", add rows (2e6), << new column ("X", character), <<new column ("y", character));
n = nitems(lis);
r=0;
for  each ( { i }, 1::(n-1), 
	for each( { j }, ( i + 1):: n, 
		r++;
		dt[ r, 1] = lis[ i ]; dt[ r, 2 ] = lis [ j ]		
	)
);

t2 = HP Time();


// nChooseK matrix solution
dt = As Table( NChooseK Matrix( N Items( lis ), 2 ), <<column names( {"x", "y"} ) );
dt << New Column( "first", character, <<set values( lis[dt:x << get values] ) );
dt << New Column( "second", character, <<set values( lis[dt:y << get values] ) );
dt << delete columns( 1 :: 2 );

t3 = HP Time();

Print( Eval Insert( "Create table of pairs from loop: ^(t2-t1)/1e6^ seconds." ) );
Print( Eval Insert( "Create table of pairs from nChooseK matrix: ^(t3-t2)/1e6^ seconds." ) );

[#10]

I should also mention that the examples I used were with strings. If you are using numbers, you can just use straight matrix ops, which are pretty fast... the 2 million row table is generated in 0.3 seconds, and the 26choose5 table in 0.04 seconds.

Names Default To Here(1);

nums = J(2e3, 1, randominteger(1e9));

t1 = hptime();

astable(shape(nums[nChoosekMatrix( 2e3, 2 )], ., 2));

t2 = hptime();

Print( Eval Insert( "Create table of 2 numbers chosen from 2000: ^(t2-t1)/1e6^ seconds." ) );

// 26 choose 5
nums = J(26, 1, randominteger(1e9));

t3 = hptime();

astable(shape(nums[nChoosekMatrix( 26, 5 )], ., 5));

t4 = hptime();

Print( Eval Insert( "Create table of 5 numbers chosen from 26: ^(t4-t3)/1e6^ seconds." ) );