- JMP will suspend normal business operations for our Winter Holiday beginning on Wednesday, Dec. 24, 2025, at 5:00 p.m. ET (2:00 p.m. ET for JMP Accounts Receivable).
Regular business hours will resume at 9:00 a.m. EST on Friday, Jan. 2, 2026. - We’re retiring the File Exchange at the end of this year. The JMP Marketplace is now your destination for add-ins and extensions.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Best method to do Failure Rate comparison
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Best method to do Failure Rate comparison
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Best method to do Failure Rate comparison
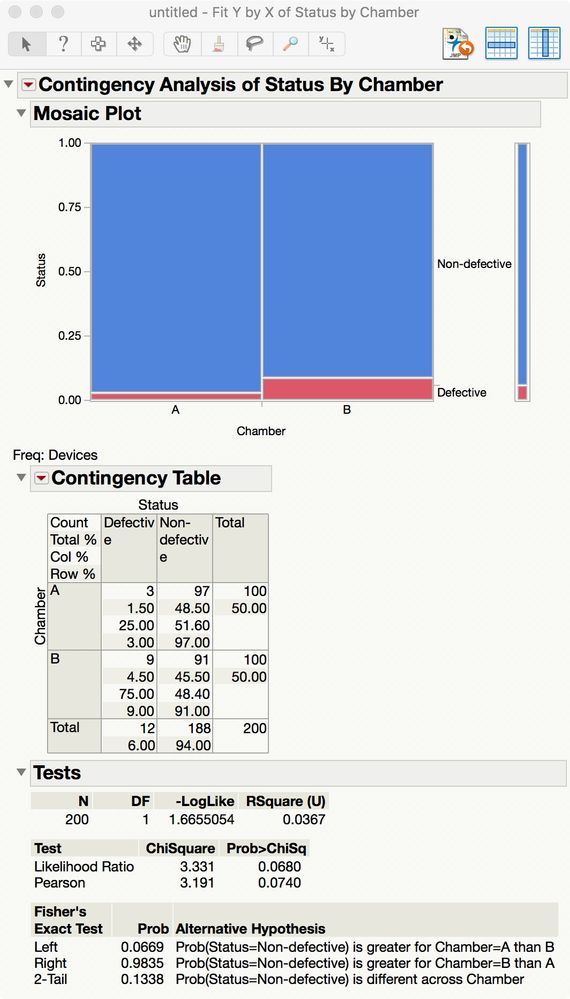
If the problem is as simple as you describe (compare two failure rates), then you can use a contingency table analysis. Try these steps:
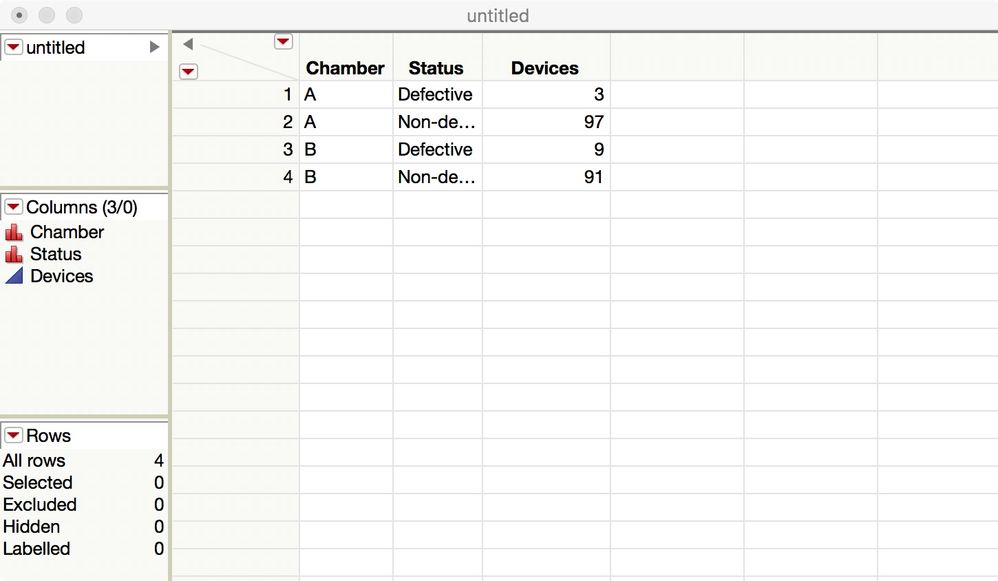
- Enter your data as Chamber (A,B), Status (Defective,Non-defective), and Devices (counts).
- Select Analyze > Fit Y by X.
- Select Status and click Y.
- Select Chamber and click X.
- Select Devices and click Freq.
Here is what my data table looks like, based on your example:
Here is the result of the analysis:
Does this approach help?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Best method to do Failure Rate comparison
Could you provide a bit more information about the kind of data you have or plan to collect? Assuming there is data for a specified time period during which some items fail and some do not, and there are multiple processes you are comparing, your data is censored - items that have not yet failed, might still fail if the experiment/process were to be run for a longer period of time. In that case, some type of survival (e.g., proporational hazards) model might be appropriate. On the other hand, if you have data that spans the lifetime of these items, during which some have failed and some have not, then a classification model could be used. So, if you provide more information about the nature of your data, a better answer can be provided.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Best method to do Failure Rate comparison
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Best method to do Failure Rate comparison
To add to Dale's reply, see Help > Books > Reliability and Survival Methods > Life Distribution. There is a feature of this platform to compare groups that is fully explained in this chapter along with examples.
This solution assumes that you have life data, censored or exact.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Best method to do Failure Rate comparison
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Best method to do Failure Rate comparison
If the problem is as simple as you describe (compare two failure rates), then you can use a contingency table analysis. Try these steps:
- Enter your data as Chamber (A,B), Status (Defective,Non-defective), and Devices (counts).
- Select Analyze > Fit Y by X.
- Select Status and click Y.
- Select Chamber and click X.
- Select Devices and click Freq.
Here is what my data table looks like, based on your example:
Here is the result of the analysis:
Does this approach help?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Best method to do Failure Rate comparison
I agree with Mark's suggestion, but make sure you know exactly what question you want to ask. Mark's continency table will answer the question whether the failure rate differs after 3 months. If you want to answer a more general question - do the failure rates differ - then your data probably is censored, meaning that you have a measurement after 3 months, but the lifetimes are actually longer. I suspect the two analyses will yield similar qualitative comparisons, but not quantitatively equivalent.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Best method to do Failure Rate comparison
Able to elaborate what do you mean by my data probably is censored?
Rgrds
Irfan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Best method to do Failure Rate comparison
From your response to Mark below, it sounds like you have observations that span a period of time during which some items fail and some do not. At the end of that time period, the question is what is that state of items that did not fail? Are they beyond the end of their useful life? Are you only interested in whether they fail within X months time? If the time period is arbitrarily chosen (that's when data collection ended), then all you know about items that have not failed is that they have not failed "yet." It is the "yet" that would make your data censored. This means that you can't claim they won't fail, only that they will not have failed at that particular time mark.
Expanding a bit further - your question to Mark below speaks of wanting to model the time to failure. This is a typical kind of survival analysis. I think there are 2 general approaches. If the items have all reached the end of their useful life, but some items have failed and they fail at different times, then your dependent variable would be the the time to failure and you would do a regression analysis (not the contingency analysis which only look at whether they fail or not, but an analysis that focuses on the time to failure). If the end of data collection is arbitrary (in the sense I describe above) then a survival analysis would be appropriate. The dependent variable is still the time to failure (it is a type of regression analysis), but your data is censored - so you would use the survival platform rather than the fit model platform.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Best method to do Failure Rate comparison
yes this sure helps, another problem that i have lets assume that for a particular chamber the high failure rate is due to some degrading parts and it is not related to the baseline performance of the chambers, is there a way for statistical analysis to screen this out. Another problem that I have is if would like to analyze the Mean time to failure which means that maybe a certain chamber is able to run until fail for 20 days while the other chamber might run and fail after every other 4 days. Do I use the contigency table as well?
Recommended Articles
- © 2025 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us