Analyzing Goodness of Fit - Shapiro-Wilk and Anderson-Darling p-Values

[#1]

Hello,

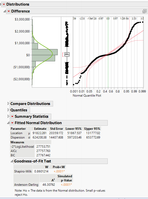
I was curious about something. I was looking at goodness-of-fit under Distributions using Fitted Normal Distribution -> Goodness-of-Fit Test and I know from what I read on interpreting the results that if the p-values are small then you reject the null and can conclude that the data is not normally distributed. So my initial look at the column was obvious that it is not normally distributed (which I expected).

 So then I tried normalizing using the Johnson Normalize and reran it with that and it didn't work. 

 So then I tried the Normal Quantile method and ran it again. At first glance I thought it worked but then I noticed that the Shapiro-Wilk p-value = 0.0027 (which would warrant rejecting the null) but the Anderson-Darling p-value = 0.1672 which does not. 

Question 1: What do you do when they conflict like that? Do they both need to provide the same conclusion? 

Question 2: Is it bad to try different methods of normalization like that? If so, do you have any suggestions for documentation or videos to help choose the best one? 

[#2 · Accepted solution]

1: They conflict because they use different math. Anderson-darling is more sensitive to deviation in the tail. From your picture it looks pretty "wavy" throughout that normal plot. So the shapiro-wilk could be picking up on that non-normal signal that's outside the tails.

2: bad? i don't know. it's an accepted strategy to explore what data transformation would work best in the situation. not sure i'd say it's bad. I do like box cox transformation more than any others when it resolves the non-normality though.

the whole setup though i think is more of an academic conversation. what even if this and why is normality testing important. Id say it almost all likelihood that any time spent on this is just extra processing and not needed for the context of a business decision. your data looks like financial numbers. and very big ones at that. so being non normal isn't that surprising.

more context might get your more replies.

[#3]

Hi @ACraig : A note about the Normal Quantile "transformation". No matter what the parent distribution is, the Normal Quantile "transformation" will, by definition, always result in a normal distribution.  It is a function of the ranks, not of the raw data. So, that is not an appropriate transformation to normality.

As @awelsh said, context is important here; why are you testing for normality?

[#4]

Hello, I really appreciate the feedback! To your question, I was wanting to run some ANOVA testing.

[#5]

Are you combining the entire dataset in the above examples? It could be differences among the subgroup means that is causing the non-normality in the combined dataset. Check the subgroups individually for normality not combined if that's the case.

Alternatively you could use some alternatives like X-bar and R charts. Or Welch's ANOVA. If this is financial data you may want to test the medians with Mann-Whitney instead of the means.

[#6]

Hi @ACraig : FWIW, and in addition to the very good comments by  @awelsh , constant variance (SD's, for each group, are similar) is more important than normality.