- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Analysis of Opt DOE simulation results
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Analysis of Opt DOE simulation results
Dear JMPer,
Currently, I'm under analysis a Opt DOE simulation results. However, I don't get consistent result form simulations and also get to different trends during counter profile analysis. I wonder if any methodology or analysis could use to understand which simulation result is valid.
Here is my simulation process. The DOE matrix is in Table 1
- Fit model (Simulation 1):
- Put 4 inputs in Simulation 1 and select surface response mode in macro functions.
- Remove interaction option from same factor, eg input A * input A
- Run the simulation with standard least squares and effect leverage.
- Table 2 shows Rsquare of summary of fit and Output trend based on Input A/C (Input A/C is key factors for the process)
- Fit two level screening (Simulation 2):
- Select Output A to run fit two level screening.
- Use defined important factors, such as output's interaction and individual outputs.
- Run the simulation with standard least squares and effect leverage.
- Table 2 shows Rsquare of Summary Of Fit and Output trend based on Input A/C (Input A/C is key factors for the process)
Output B and Output C is able to predict the trend based on higher input or lower input (due to physic). However, Output A is the important response that I would like to see what simulation would show the trend. Based on Rsquare of Summary Of Fit, Simulation 1 seems batter than Simulation 2. However, output trend of Simulation 2 is more logical to me than Simulation 1. Therefore, I wonder if anyone could share some input to have better analysis for both simulation results. Please kindly share me your inputs. Much appreciate your time and help.
Thank you,
Bests,
Andy
Table 1. DOE matrix
| Leg# | Pattern | Input A | Input B | Input C | Input D | Input E | Input F | Output A | Output B | Output C |
| 1 | +−−++− | 300 | 200 | 100 | 3 | 25 | 1 | 0.0% | 2,463 | 61 |
| 2 | −+−+−+ | 200 | 400 | 100 | 3 | 15 | 5 | 0.0% | 3,572 | 45 |
| 3 | ++−−++ | 300 | 400 | 100 | 1 | 25 | 5 | 0.0% | 3,990 | 47 |
| 4 | −−−−−− | 200 | 200 | 100 | 1 | 15 | 1 | 0.0% | 3,245 | 31 |
| 5 | +−−−−+ | 300 | 200 | 100 | 1 | 15 | 5 | 0.0% | 3,017 | 34 |
| 6 | −−−+++ | 200 | 200 | 100 | 3 | 25 | 5 | 0.0% | 3,842 | 76 |
| 7 | −+−−+− | 200 | 400 | 100 | 1 | 25 | 1 | 0.0% | 3,431 | 48 |
| 8 | ++−+−− | 300 | 400 | 100 | 3 | 15 | 1 | 0.0% | 2,409 | 51 |
| 9 | 000000 | 250 | 300 | 110 | 2 | 20 | 3 | 0.0% | 3,336 | 66 |
| 10 | 000000 | 250 | 300 | 110 | 2 | 20 | 3 | 0.0% | 2,564 | 66 |
| 11 | −++++− | 200 | 400 | 120 | 3 | 25 | 1 | 0.0% | 3,289 | 62 |
| 12 | −−+−++ | 200 | 200 | 120 | 1 | 25 | 5 | 0.0% | 2,698 | 53 |
| 13 | +−++−+ | 300 | 200 | 120 | 3 | 15 | 5 | 0.0% | 3,017 | 47 |
| 14 | +++−−− | 300 | 400 | 120 | 1 | 15 | 1 | 0.0% | 3,460 | 31 |
| 15 | −++−−+ | 200 | 400 | 120 | 1 | 15 | 5 | 2.8% | 3,503 | 28 |
| 16 | −−++−− | 200 | 200 | 120 | 3 | 15 | 1 | 0.0% | 2,835 | 42 |
| 17 | +−+−+− | 300 | 200 | 120 | 1 | 25 | 1 | 0.0% | 2,304 | 42 |
| 18 | ++++++ | 300 | 400 | 120 | 3 | 25 | 5 | 0.0% | 3,431 | 69 |
| 19 | POR | 150 | 300 | 120 | 0 | 0 | 0 | 7.1% | 3,642 | 16 |
| 20 | POR | 150 | 300 | 120 | 0 | 0 | 0 | 8.3% | 3,093 | 15 |
Table 2. Simulation 1 and Simulation 2 Results.
| JMP analysis | Simulation 1 | Simulation 1 | Simulation 1 | Simulation 2 | Simulation 2 | Simulation 2 |
| Matrix | Output A | Output B | Output C | Output A | Output B | Output C |
| Input A high | Reduce | reduce | two trends | increase | Increase | reduce |
| Input A low | increase | increase | two trends | reduce | Reduce | Increase |
| Input C high | Increase | Increase | reduce | reduce | Increase | Reduce |
| Input C low | reduce | reduce | increase | increase | reduce | increase |
| Summary of fit Rsquare | 0.96 | 0.78 | 0.84 | 0.95 | 0.59 | 0.85 |
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Analysis of Opt DOE simulation results
You asked, "Based on your experience, should the simulation be focused on main effects which has defined by fit two level screening?"
First of all, this is NOT a simulation. It is a regression analysis to fit a linear model.
There are several common ways to approach the analysis of an experiment based on a fractional factorial design. You can approach it, as I said, using two stages in which you first select the main effects, believing that the principles of hierarchy holds, and then, add interaction terms for the active factors, believing that the principle of heredity holds. This approach is often a successful way to select the model. This model, like all others, must be verified with new empirical observations (augmented runs).
You asked, "Could you share me script for stepwise platform simulation?"
You do not need a script. Start your analysis with Fit Model as usual. Specify the response data column in the Y role. Specify the terms in the linear predictor for the Effects. But switch the Personality from Standard Least Squares to Stepwise..
Please see JMP > Books > Fitting Linear Models > Stepwise chapter.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Analysis of Opt DOE simulation results
So you designed an experiment for a computer simulation? That is, the factor levels are used as parameter values in the computer simulation?
I instead interpret your question to be about regression results. The two-level fractional factorial design in 16 runs with 2 center points and 2 ad hoc runs does not support estimating the full quadratic model. In this case, you must not try to estimate the parameters for the quadratic terms.
The Screening platform is intended only for two-level factors. You used a two-level design but you added a third or fourth level with the center points and ad hoc runs. This platform won't necessarily give you wrong information but it won't necessarily give you correct information when there are more than two levels.
Still, it can be useful as an exploration tool and a starting point leading to a full regression analysis. I used it to find a model for Output A with the linear predictor including Input E, Input D, Input A, and Input E*Input E. So it detected a non-linear response but attributing it to Input E is arbitrary. It is based on the heredity principle and nothing more. It cannot be established with this experiment. Output B does not appear to have any fixed effects from these factors. Output C has the most complex model. It includes two quadratic effects, which is the most that might be estimated and the choice of which terms is again arbitrary. The usual action at this stage is to augment the two-level design specifically to estimate all the quadratic terms for a final decision.
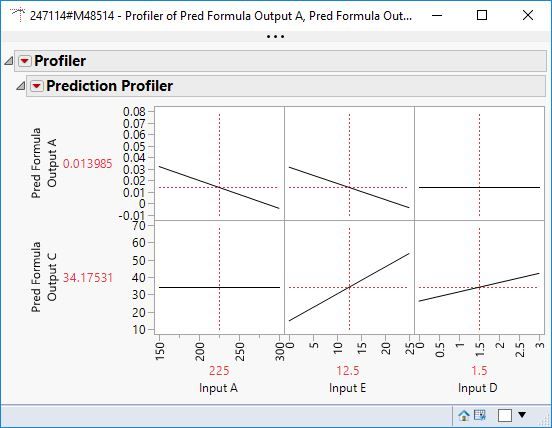
Another approach is to use the Stepwise platform starting with all the potential terms (main effects and interactions) that might be estimated. Here is the prediction profiler launched with the model formulas saved for Output A and Output C using stepwise regression to select the model.
Another approach is to start with the main effects only, remove the unimportant factors, then add and test interactions involving the important factors. This approach is based on the hierarchy and heredity principles.
Just remember that there are many confounded and correlated effects using this design. It provides incomplete information about the response. So augmentation might be the best next step to clarify the important effects. Regardless, the final model selected here or after augmentation must be empirically verified with new, independent runs for as yet untested treatments.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Analysis of Opt DOE simulation results
@Mark_Bailey Thanks a lot for your detail explanation. I acknowledged inputs for the current matrix design.
The DOE matrix is designed for fractional factorial with some 2-factor interactions and I tried to define key factors for the process.
A quick question. Based on your experience, should the simulation be focused on main effects which has defined by fit two level screening? I notice that you would analyze the defined effects and plot prediction profile.
Also, I haven't use stepwise platform before. Could you share me script for stepwise platform simulation?
Once again, thanks for your thoughts and inputs.
Thank you,
Bests,
Andy
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Analysis of Opt DOE simulation results
You asked, "Based on your experience, should the simulation be focused on main effects which has defined by fit two level screening?"
First of all, this is NOT a simulation. It is a regression analysis to fit a linear model.
There are several common ways to approach the analysis of an experiment based on a fractional factorial design. You can approach it, as I said, using two stages in which you first select the main effects, believing that the principles of hierarchy holds, and then, add interaction terms for the active factors, believing that the principle of heredity holds. This approach is often a successful way to select the model. This model, like all others, must be verified with new empirical observations (augmented runs).
You asked, "Could you share me script for stepwise platform simulation?"
You do not need a script. Start your analysis with Fit Model as usual. Specify the response data column in the Y role. Specify the terms in the linear predictor for the Effects. But switch the Personality from Standard Least Squares to Stepwise..
Please see JMP > Books > Fitting Linear Models > Stepwise chapter.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Analysis of Opt DOE simulation results
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Analysis of Opt DOE simulation results
An alternate approach to Mark's method of model building (starting with 1st order then adding 2nd order based on excellent principles of scarcity, hierarchy and heredity) is to start with a saturated model. Use Daniel plots (normal/half normal), Pareto plots (making sure the estimates are of practical significance) and Bayes plots (if your into that sort of thing). Remove insignificant terms (consider Rsquare vs. Rsquare adjusted deltas), and re-run the model paying particular attention to residuals to ensure your model meets the usual assumptions.
One of my favorite quotes:
"Two equally competent investigators presented with the same problem would typically begin from different starting points, proceed by different routes, and yet could reach the same answer. What is sought is not uniformity but convergence" (Box, Hunter Hunter "Statistics for Experimenters").
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us