- JMP will suspend normal business operations for our Winter Holiday beginning on Wednesday, Dec. 24, 2025, at 5:00 p.m. ET (2:00 p.m. ET for JMP Accounts Receivable).
Regular business hours will resume at 9:00 a.m. EST on Friday, Jan. 2, 2026. - We’re retiring the File Exchange at the end of this year. The JMP Marketplace is now your destination for add-ins and extensions.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Analysing 2-factor 2-level design as if it was 4 different treatment design
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
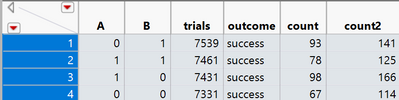
Analysing 2-factor 2-level design as if it were 4 different treatment design
Hello!
Just curious why we see different results in such cases.
Here we have a classic 2-factor 2-level factorial design which we can analyze using Nominal regression/logistic regression.
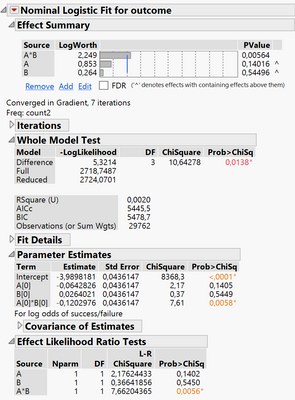
Analysis shows that only interaction is significant :
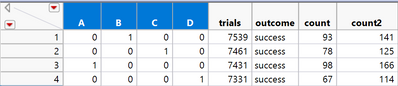
However, if we transform this data as if there were 4 factors A1, B1, C (A1*B1), D (A0*B0),
then we will see that main effects are significant.
How can we explain and interpret this?
PS
Datasets are in attachments. These results are from real experiment.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Analysing 2-factor 2-level design as if it was 4 different treatment design
You do not really have four factors. Your construction over-specifies the model, so JMP arbitrarily zeros the last 'factor' and indicates that the first three are biased.
The equivalent to two two-level factors would be one four-level factor, not four two-level factors.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Analysing 2-factor 2-level design as if it was 4 different treatment design
Yep, as Mark says...you have 3 degrees of freedom in 4 treatments.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Analysing 2-factor 2-level design as if it was 4 different treatment design
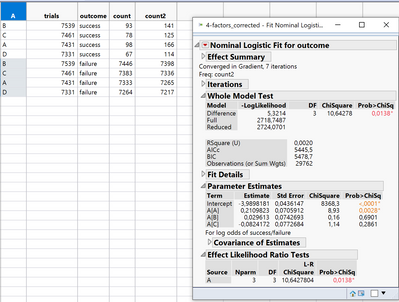
I am sorry.
I have corrected the file to 1-factor 4-level. Now it shows that level A (which is factor A) is significant:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Analysing 2-factor 2-level design as if it was 4 different treatment design
Why are you doing this way? It is more informative to treat this case as two independent factors that might interact in the effect of the response. The original linear predictor with A + B + A*B makes the most sense.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Analysing 2-factor 2-level design as if it was 4 different treatment design
If we look at treatment A1 B0 it has the highest success rates for both count and count2.
Interaction A1 B1 has the lowest success rates if we don't include the control A0 B0.
So my intuition says that A1 should me practically significant factor which has the biggest impact. Is my intuition in the right direction?
I may assume that there is not enough sample size for detecting the effect of factor A, but a smaller interaction effect was detected as significant.
So does it mean that factor A doesn't have effect by its own...
That's why I looked at it as 1-factor 4-level, and it supported my assumption that A is significant.
I don't have a degree in Statistics (I am a self learner from a different field) and the results above confuses my mind :)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Analysing 2-factor 2-level design as if it was 4 different treatment design
I haven't looked at your data, but it appears the effect of A depends on B (or B depends on A). This we call an interaction effect. The interaction has greater effect than the main effect by itself.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us