JMP를 활용한 Reed–Muench 방법론 적용

[#1]

Reed–Muench method is the simplest and most intuitive way to determine an endpoint in a biological procedure.

The above methodology was published in The American Journal of Hygiene in 1937. A Simple Method of Estimating Fifty Per Cent Endpoints This is the methodology described in the paper.

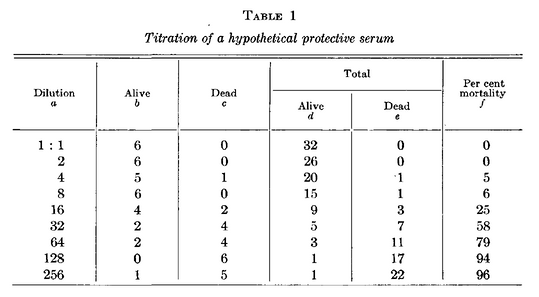
Make the data presented in the thesis into a JMP Data Table. In the data corresponding to Table 1 of the paper, the data corresponding to dilution is quantified through log transformation.

To create a variable called Log(Dilution) in the red box above, you need to create a simple formula (JSL Code) as shown below.

Log10(
 Num( Substr( :Dilution, 3, 3 ) ) /
 Num( Substr( :Dilution, 1, 1 ) )
)

After getting the 3-digit value from the 3rd digit in the dilution variable, take the Log10 value.

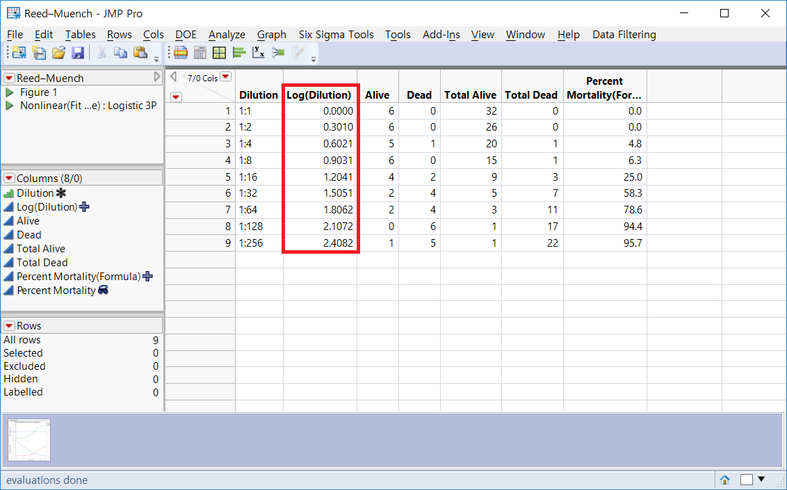
After performing the above operations, use Log (Dilution) on the X axis and Percent Mortality on the Y axis to fit the curve using JMP Graph Builder. Below that, a graph of overall survival/death is also shown.

The endpoint we want to find here is Dilution, where the Percent Mortality value is 50%. In the actual paper, interpolation was used to calculate manually, but here, we will use JMP's Nonlinear Modeling method to find the value.

To use this method, select Analyze >> Specialized Modeling >> Nonlinear menu.

It goes through the following steps:

One. Nonlinear Fitting (Logistic or Probit or Weibull, etc.)

2. Estimating the Log(Dilution) value at which the percent mortality is 50% through inverse estimation

3. Transform to return the log transformation value.

in the order above

One. Nonlinear Fitting

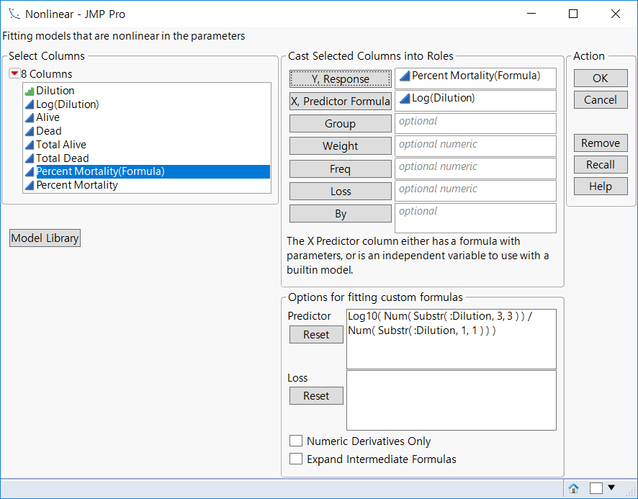
Specify Percent Mortality for Y response and Log(Dilution) for X Predictor Formula.

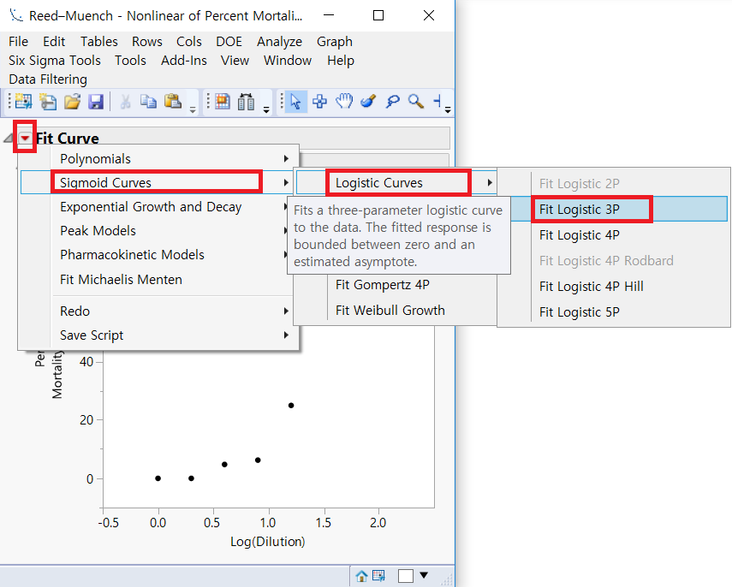
Press the Hot Spot (Red Triangle) on the left side of the Fit Curve and select Sigmoid Curve >> Logistic Curves >> Fit Logistic 3P. Alternatively, fitting is possible with Probit or Weibull.

2.Log (Dilution) value estimation that satisfies 50% percent mortality through inverse estimation

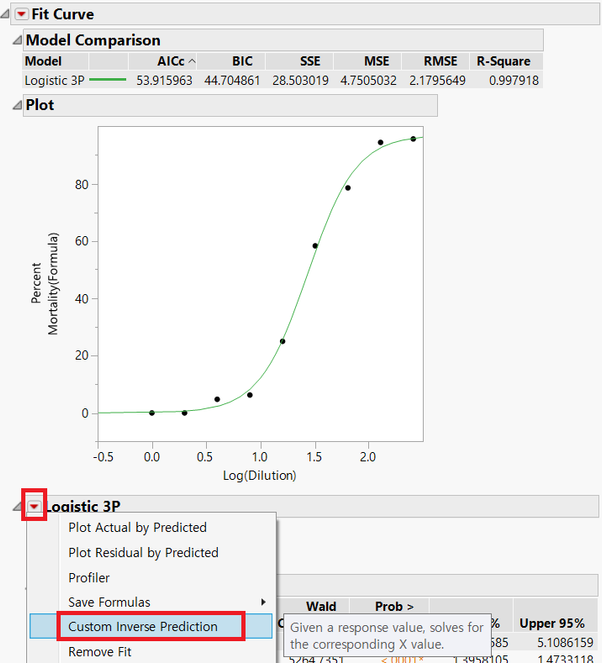
Click the Hot Spot on the left side of Logistic 3P and select Custom Inverse Prediction

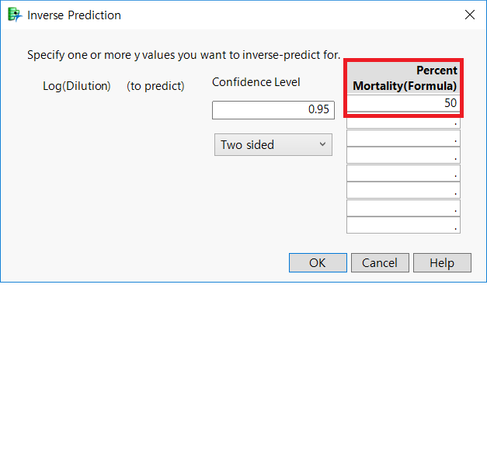
Enter the desired value (50%) in the red box above.

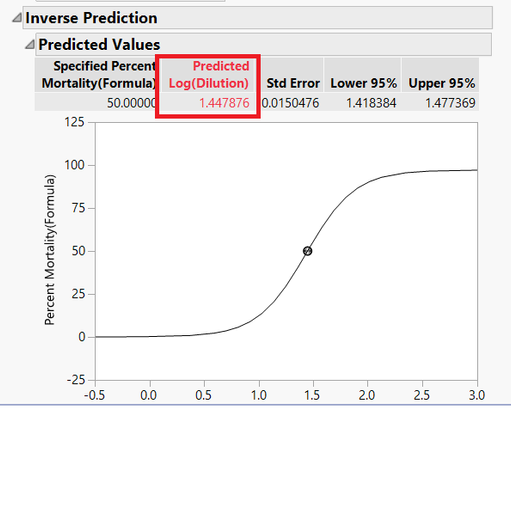
This gives you the desired value of 1.447876.

Using this to get 10^(1.447876) for the next step 3, the conversion, we get 28.05.

in other words, 1:28 This becomes the Dilution endpoint where the Percent Mortality becomes 50%.