- JMP User Community
- :
- JMP Users Groups
- :
- JMP Users Groups in North America
- :
- Wasatch Front JMP Users Group
- :
- Forum
- :
- Time Series Analysis - Seasonal Variation Modeling
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Time Series Analysis - Seasonal Variation Modeling
One thing common to almost all manucturing plants is Statistical Process Control. How well a site a consistently make the same product over and over again can be the difference between a mediocer company and a great one. One key to that process is looking for shifts or trends in the data. Although not commonly used, Time Series Analysis can be a helpful tool along the journey of variation reduction.
The time series analysis platform in JMP can be accessed under Analyze > Modeling > Time Series
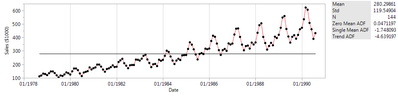
Let’s take a look at one data from the sample data. Go to Help > Sample Data. Then click on the Time Series drop down and go to Monthly Sales. Open the Time Series platform and select the Sales($1000) column with Date as the Time Series.
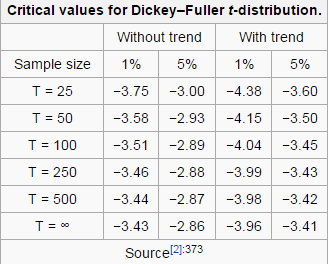
As usual in JMP, right off the bat we have some test statistics to tell us something about this data. Notice the Zero Mean ADF, Single Mean ADF and Trend ADF stats in the table to the right of the graph. ADF stands for Augmented Dickey Fuller test, which is a way to check for a unit root (a feature which changes over time) within the time series. In lamen’s terms, it’s checking for an underlying time dependent trend within the data. The three metrics correspond to checking for no underlying time component (zero mean), constant increase over time (single mean) and acceleration over time (Trend). If the statistic is below the T value found below then the null hypothesis that it is not a component can be rejected. In other words, if it’s below the T value then there is an underlying time component.
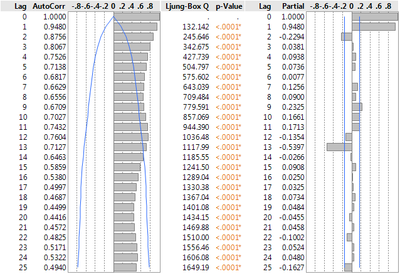
Underneath the first graph you’ll find an AutoCorrelation summary. It shows how each point is dependent on the previous points.
Noticing the clear cyclical pattern could lead one to try a Seasonal Exponential Smoothing Fit to predict the data. Go to the Red Triangle > Smoothing Model > Seasonal Exponential Smoothing.
Model Summary
DF | 129 | ||
Sum of Squared Errors |
| ||
Variance Estimate |
| ||
Standard Deviation |
| ||
Akaike's 'A' Information Criterion |
| ||
Schwarz's Bayesian Criterion |
| ||
RSquare |
| ||
RSquare Adj |
| ||
MAPE |
| ||
MAE |
| ||
-2LogLikelihood |
| ||
Stable | Yes | ||
Invertible | No | ||
Parameter Estimates
Term | Estimate | Std Error | t Ratio | Prob>|t| |
Level Smoothing Weight |
| <.0001* | ||
Seasonal Smoothing Weight |
| <.0001* |
I hope this helps you in your exploration of time series data. Please leave a comment if you have any questions about time series analysis or any great Time Series stories to share. Thanks!
- © 2024 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- About JMP
- JMP Software
- JMP User Community
- Contact