- JMP User Community
- :
- Blogs
- :
- Uncharted
- :
- Tracing Pictures
- Subscribe to RSS Feed
- Mark as New
- Mark as Read
- Bookmark
- Subscribe
- Printer Friendly Page
- Report Inappropriate Content
@lwx228 asked how to make formulas that make images. I didn't get all the way to the bottom (like the beautiful animation here), but I got close.
Load an image and use the Canny filter to find some boundaries between light and dark. The closer to a single closed loop, the better for what follows. The discontinuity below will show artifacts later, but not too bad.

//clear globals();// uncomment this if you change the picture 3 or 4 lines down to make it reload...
If( Try( Type( original ) != "Picture", 1 ), // set to 1 long enough to download once
original = Open(
//"https://i.stack.imgur.com/wtJoA.png", // this was an elephant...the loop closes nicely
// this fish does not close the loop...
"https://upload.wikimedia.org/wikipedia/commons/thumb/8/8b/Malayan_fishes_%28PLATE_LXX%29_BHL46234933.jpg/800px-Malayan_fishes_%28PLATE_LXX%29_BHL46234933.jpg", // https://commons.wikimedia.org/wiki/File:Malayan_fishes_(PLATE_LXX)_BHL46234933.jpg
"png"
);
Beep();// comment out the clear globals to prevent re-loading the image over the internet each time
);
New Window( "Original Image", original );
bitmap = New Image( original );
bitmap << filter(
"canny", // TWEAK THESE for different images; you want a single loop for best results
largeThreshold( .5 )/*tracing begins when a large-value edge is found*/,
smallThreshold( .01 )/*tracing stops when the edge value gets too small*/,
radius( 2 )/*a blur-filter, use 0 for no blurring*/,
Repeat( 3 )/* number of repeats of a box-blur; 3 approximates a gaussian-blur filter */
);
New Window( "Original Edge Detection", bitmap );Above, the code has a commented clear globals() that will reset the variable holding the image and cause it to reload when the try() detects there is no image. You can switch to the elephant image a few lines down. The beep will remind you to re-comment the clear globals. The first NewWindow() shows the original image. The bitmap is then copied from the original and filtered. The Canny filter is an edge-finder-follower with parameters that must be tweaked for each image. Both images above work with these settings (because the elephant is too easy.) The final newwindow() shows the outline.
Unfortunately, the outline is in a bitmap. The code that follows needs a list of x,y coordinates that form a continuous loop.
bitmap = bitmap << getpixels;
nr = N Rows( bitmap );
nc = N Cols( bitmap );
points = Loc( bitmap );
// see https://community.jmp.com/t5/JSL-Cookbook/Using-Loc-with-a-2D-Matrix/ta-p/195207
rowlocs = Floor( (points) / nc ) + 1; // nc is the number of columns in the 2D pixmat
collocs = Mod( (points), nc ) + 1; // rowlocs and collocs are 2D indexes (1-based)
// center and scale
rowlocs = rowlocs - Min( rowlocs );
rowlocs = rowlocs / Max( rowlocs );
rowlocs = rowlocs * 2 - 1;
collocs = collocs - Min( collocs );
collocs = collocs / Max( collocs );
collocs = collocs * 2 - 1;Above, get the pixels into a matrix named bitmap, and the number of rows and cols in nr and nc. Use the loc() function to locate the non-zero pixels. Black is zero, white is one in the filtered picture. Loc returns indexes that work, but they assume the bitmap is one column of nr*nc. For tracing the outline it will be better to have the x,y indexes. rowlocs and collocs are calculated with a formula from here. Go ahead and scale the indexes into a -1 to 1 space...they won't be used for indexing because they only point to ones in the bitmap. But they will be used for neighbor testing.
// extract the line-loop. crude, probably slow... first thing that comes to mind...
kdt = KDTable( rowlocs || collocs );
idxSort = J( N Rows( points ), 1, . );
idx = (kdt << K nearest rows( 1, [0, 0] ))[1][1];
idxSort[1] = idx;
For( i = 2, i <= N Rows( points ), i += 1,
kdt << removerows( idx ); // remove this point from the table so
idx = (kdt << K nearest rows( 1, idx ))[1][1]; // can find the next one
idxSort[i] = idx; // save a sorted list of the indexes
);You can probably think of other ways to do what this code does, maybe faster. It builds a nearest-neighbor table of the 2D coordinates, finds a starting coordinate (closest to 0,0, which could have been anywhere else), then records the chain of nearest neighbors by removing each one as it is found and using the removed coordinate to find the next. It will skip over gaps as needed. Make a graph to check everything is working.
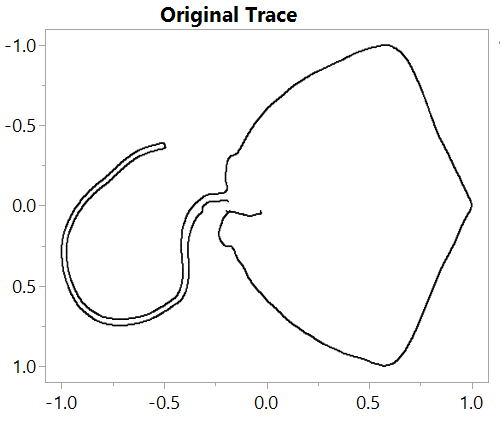
// put the row/col in connected order
rowlocs = rowlocs[idxSort];
collocs = collocs[idxsort];
dt = As Table( rowlocs || collocs );
dt << setdirty( 0 );
dt << Graph Builder(
Size( 514, 444 ),
Show Control Panel( 0 ),
Variables( X( :Col2 ), Y( :Col1 ) ),
Elements( Points( X, Y, Legend( 4 ) ) ),
SendToReport(
Dispatch( {}, "Col1", ScaleBox, {Min( 1.1 ), Max( -1.1 )} ),
Dispatch( {}, "graph title", TextEditBox, {Set Text( "Original Trace" )} ),
Dispatch( {}, "Graph Builder", FrameBox, {Marker Size( 0 )} )
)
);The first two statements above use the indexes saved previously to sort the row and col indexes into order. AsTable makes a data table from the two-column matrix made by concatenating row and col indexes. GraphBuilder makes the picture. Use the table to select the points in order and verify that the loop in the graph draws from beginning to end, not top to bottom.
The rest consists of a formula I do not understand well and a bunch of displaybox work.
// run the fft
{colx, coly} = FFT( {collocs} );
{rowx, rowy} = FFT( {rowlocs} );
//dt=astable(colx||rowx);dt<<setdirty(0);
nkeep = 20; // default
nkeepscaled = nkeep ^ .5; // make the slider have more resolution at the low end
nIterp = 100;
// Yusuke's formula. I don't understand why cos() - sin() works.
// https://community.jmp.com/t5/Documents/FFT-cos-sin-jsl/ta-p/23266
rebuild = Function( {nn},
x1 = y1 = J( nIterp, 1, 0 ); // bigger for more interpolated points
n = N Rows( points );
For( s = 1, s <= N Rows( x1 ), s++,
t = Interpolate( s, 1, 1, N Rows( x1 ), n );
colsum = 0;
rowsum = 0;
For( k = 1, k <= nn, k++,
colsum += (1 / n) * (colx[k] * Cos( (k - 1) * 2 * Pi() / n * (t - 1) ) - coly[k] * Sin( (k - 1) * 2 * Pi() / n * (t - 1) ));
rowsum += (1 / n) * (rowx[k] * Cos( (k - 1) * 2 * Pi() / n * (t - 1) ) - rowy[k] * Sin( (k - 1) * 2 * Pi() / n * (t - 1) ));
);
y1[s] = rowsum;
x1[s] = colsum;
);
);
rebuild( nkeep );
New Window( "Example",
V List Box(
gb = Graph Box(
Frame Size( 600, 500 ),
X Scale( -1, 1 ),
Y Scale( -1, 1 ),
yaxis( {Reversed Scale} ),
Pen Color( "Blue" );
Line( x1, y1 );
Text( {-0.9, 0.9}, "outline using " || Char( 4 * nkeep ) || " numbers" );
),
V List Box(
H List Box(
Global Box( nkeep ),
Slider Box(
1,
N Rows( points ) ^ .5,
nkeepscaled,
// start of slider script
nkeep = Min( N Rows( points ), Floor( (nkeepscaled ^ 2) ) + 1 );
rebuild( nkeep );
gb << reshow;//
, // end of script
setwidth( 500 )
)
),
H List Box(
Global Box( nIterp ),
Slider Box(
1,
2000,
nIterp,
// start of slider script
rebuild( nkeep );
gb << reshow;//
, // end of script
setwidth( 500 )
)
)
)
)
);There are two fft() calls, one for the X axis and one for the Y axis. The rebuild() function is rebuilding a pair of matrices used by the graphbox() line() function. The nInterp slider controls how many points will be interpolated back out of the FFT data and the nKeep slider determines how many bins of fft data will be kept for each interpolated point.

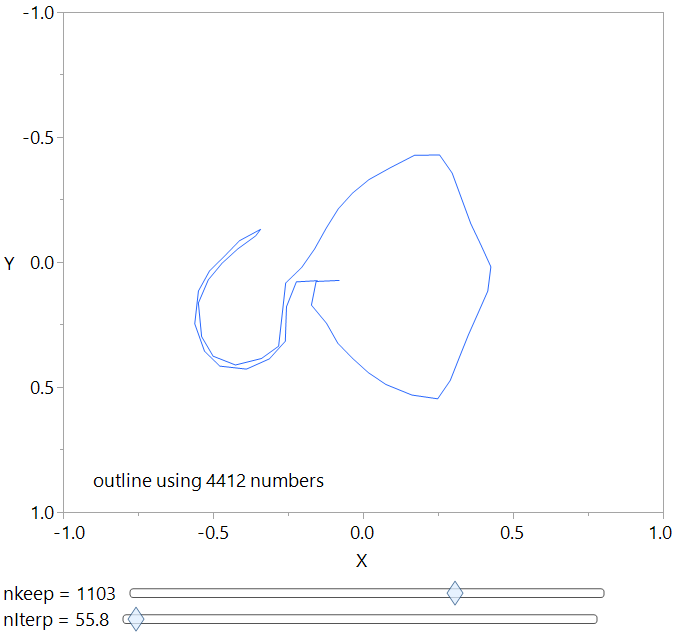
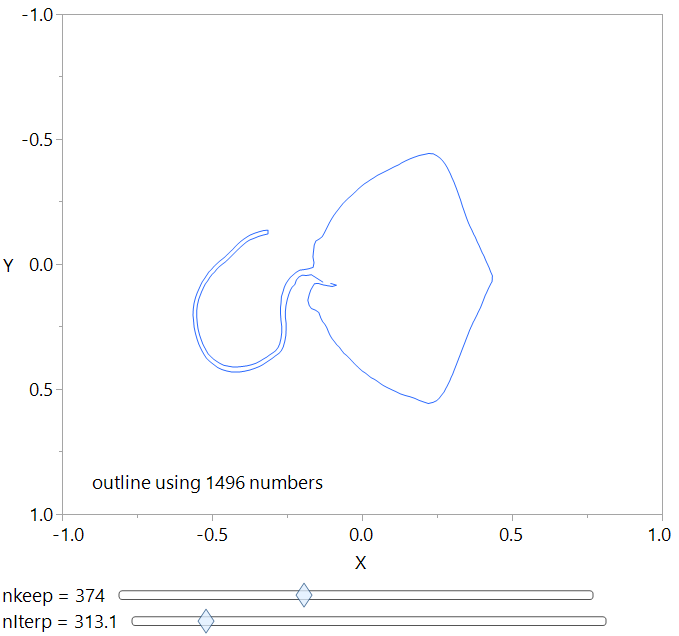
That was fun! If someone want to post more on FFTs and getting those nifty circles, that would be great!
You must be a registered user to add a comment. If you've already registered, sign in. Otherwise, register and sign in.
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us
