Update 24Dec2018: this JSL depends on a JMP 15 change to the Mandelbrot function that returns fractional iterations.
I'm playing with some JSL to follow a contour through the Mandelbrot set. Line following robots use two sensors straddling the line to decide which wheels to speed up and slow down to keep the line centered between the sensors. Right angle turns can be hard for a mechanical robot. This JSL robot uses additional sensors and creeps along slowly to capture these nearly 180 degree turns. It's moving right-to-left; there is some really tough territory just ahead. I'll know if it gets stuck in a loop or makes it into positive-Y territory soon. (No, it got caught in a twisty area again. Never made it to the North!)
Broken toy attached. If you fix it, post back, thanks!
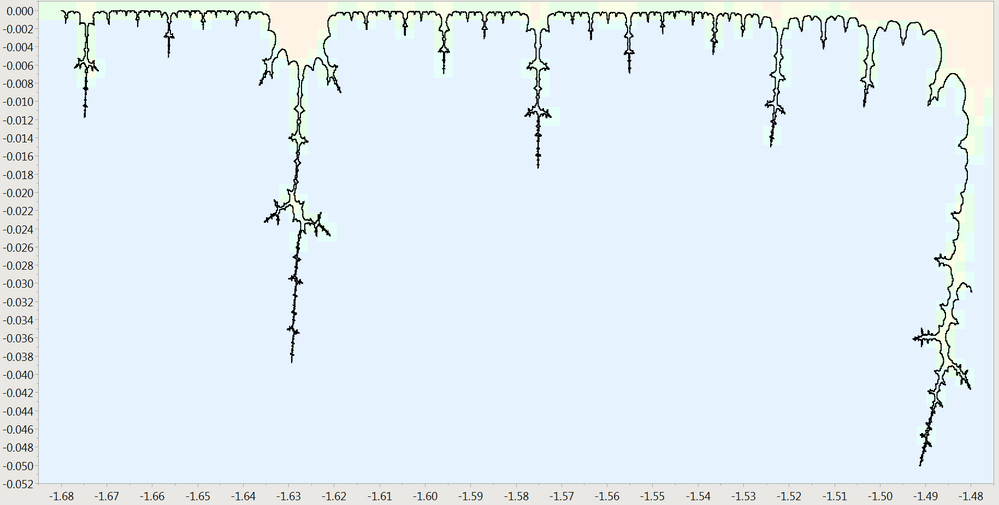 Robot following contour 25 from right to left. Hard turn ahead!
Robot following contour 25 from right to left. Hard turn ahead!
It failed on the diamond marker; probably tweaking the delta even smaller...which makes it even slower...might make it go a bit further.
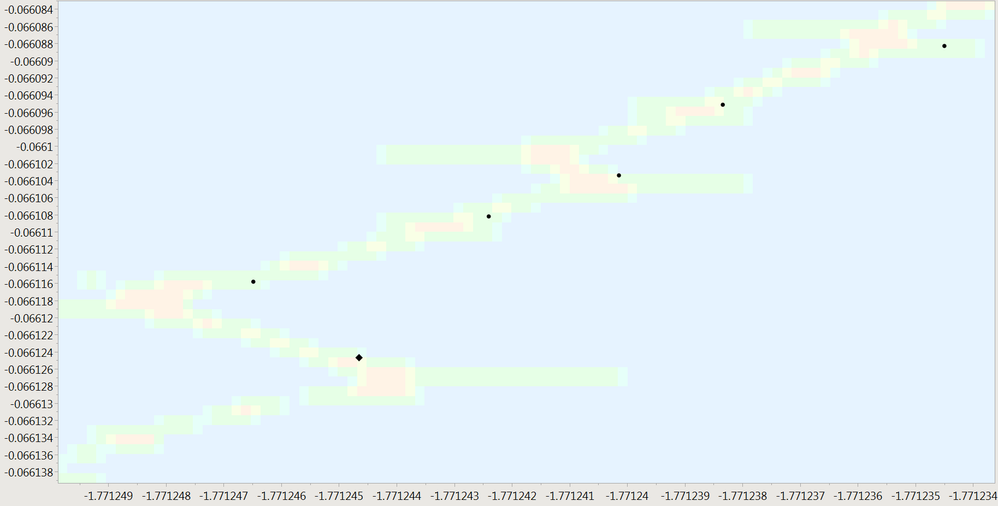 Line follower failed when it reached the diamond
Line follower failed when it reached the diamond
The attached JSL uses the minimize function to find a starting point, Graph Builder to show an updating display, add Graphic Script to put the background behind the data points using Gradient Function, and X Origin, Y Origin, X Range, Y Range to give the graphic script access to the graphs axis settings. It also uses add Rows to build a data table and Select Where and Delete Rows to manage the size of the data table.
mandelbrotLineFollower2.jsl