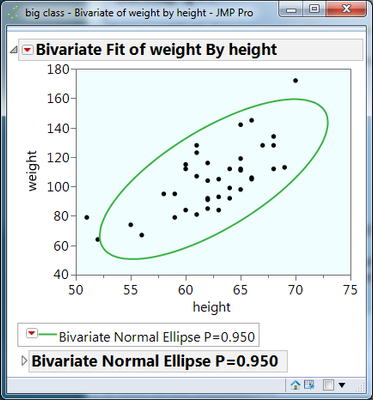
DavidK asked about drawing the ellipses around data points. I struggled through this a while back and this is a summary of what I puzzled out with help from people that actually know what they are doing. All the mistakes here are mine, comments and corrections welcome! This picture is the output from Bivariate, produced at the very end of the script. The goal of the script is to calculate the parameters to draw the green ellipse. The script uses JMP's built-in functions Correlation, Mean, StdDev, Eigen to do the work. Eigen, in particular, returns the parameters that describe the ellipse. Those parameters are turned into a 2D 3x3 transform matrix which is then used to transform points on a unit circle around 0,0 into the desired ellipse.
x = Open( "$sample_data\big class.jmp" );
H = x:height << get values; // column vectors
W = x:weight << get values;
data = H || W; // 2 columns by 40 rows
corr = Correlation( data );
mean = Mean( H ) || Mean( W );
stddev = Std Dev( H ) || Std Dev( W );
cov = Diag( stddev ) * corr * Diag( stddev );
{D, E} = Eigen( cov );
// sort columns of E. Don't know why; it controls which ellipse axis goes with the bigger vector, I think.
// you can see the gap in the ellipse change position if you use [1,2] (or just comment the next 3 lines)
jj = [2,1];
E = E[ 0, jj ];
D = D[ jj ];
// there seems to be a lot of opinions on how to do the confidence limit...
NormalContour = sqrt(ChiSquare Quantile( 0.95, 2 ));
T = NormalContour * E * Diag( Sqrt( D ) );
m = (T` |/ mean) || [0, 0, 1]; // transform matrix
unitCircle = J(100,3); // 2x2 transform uses 3x3 matrix for homogeneous coords
For( i = 1, i <= 100, i++,
unitCircle[i, 1] = Sin( (i - 1) * 2 * Pi() / 100 ); // divide by 99 to close the gap
unitCircle[i, 2] = Cos( (i - 1) * 2 * Pi() / 100 );
unitCircle[i, 3] = 1;
);
ellipse = unitCircle * m; // draw the ellipse as a unit circle transformed by m
New Window( "Ellipse from Eigen Values and Vectors",
Graph Box(xscale(50,75),yscale(40,180),
Marker( Marker State( 12 ), H, W ),
line( ellipse[0,1], ellipse[0,2])
)
);
// for comparison...
x<<Bivariate(
Y( :weight ),
X( :height ),
Density Ellipse( 0.95, {Line Color( {57, 177, 67} )} ),
SendToReport(
Dispatch( {}, "1", ScaleBox, {Format( "Fixed Dec", 12, 0 ), Max( 75 )} ),
Dispatch( {}, "2", ScaleBox, {Format( "Fixed Dec", 12, 0 ), Min( 40 )} )
)
);
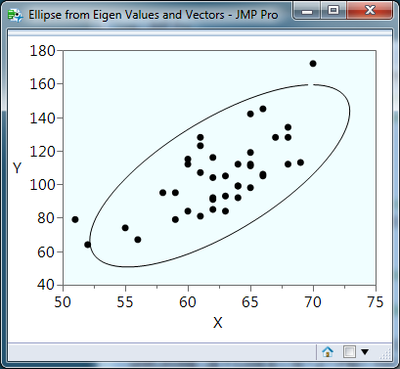
Here's the "manually" drawn ellipse. The transform matrix, m, could also be used (with its inverse) to convert data points into a unit circle; the distance from 0,0 would be less than one for points inside the ellipse. Notice that Bivariate already does all the work, including selecting the points inside or outside the ellipse.
If you use the transform matrix with JMP's Scene3D you may need to transpose "m" to match Scene3D's expectations for a transform matrix.
edit 30Sep2017: repair formatting