Circle through three points

[#1]

@lwx228 asked:   The question is a geometry question about the circle through three points. JSL attached.

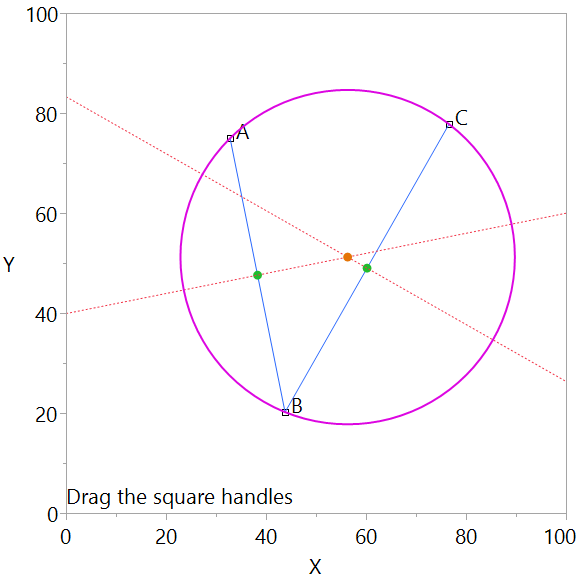Graph with three movable points, A, B, C that draws a circle through the points

The graph shows three square black handles for the points A, B, and C. Drag them around. It shows two blue lines, A and C. It shows their green midpoints and their dotted orange perpendicular bisectors. It shows the orange point where the bisectors intersect. And it shows the magenta circle with center and radius to go through A, B, and C.

// https://www.geeksforgeeks.org/program-for-point-of-intersection-of-two-lines/
lineLineIntersection = Function( {Ax, Ay, Bx, By, Cx, Cy, Dx, Dy},
	{a1, b1, c1, a2, b2, c2, determinant, x, y}, // locals
	// Line AB represented as a1x + b1y = c1 
	a1 = By - Ay;
	b1 = Ax - Bx;
	c1 = a1 * (Ax) + b1 * (Ay); 
  
    // Line CD represented as a2x + b2y = c2 
	a2 = Dy - Cy;
	b2 = Cx - Dx;
	c2 = a2 * (Cx) + b2 * (Cy); 
  
	determinant = a1 * b2 - a2 * b1; 
  
	If( determinant == 0, 
    
        // The lines are parallel. This is simplified 
		// by returning a pair of FLT_MAX 
		{., .}; // return
	, // else
		x = (b2 * c1 - b1 * c2) / determinant;
		y = (a1 * c2 - a2 * c1) / determinant;
		Eval List( {x, y} );// return 
	); 
	
); 

New Window( "Example",
	ax = 20,
	ay = 50;
	bx = 30;,
	by = 70;
	cx = 90;,
	cy = 20;
	Graph Box(
		Frame Size( 500, 500 ),
		Text( {0, 2}, "Drag the square handles" );
		Handle(
			ax,
			ay,
			ax = x;
			ay = y;
		);
		Handle(
			bx,
			by,
			bx = x;
			by = y;
		);
		Handle(
			cx,
			cy,
			cx = x;
			cy = y;
		);
		//Circle( {0, 0}, Sqrt( exx * exx + exy * exy ) );
		Text( {ax, ay}, " A" );
		Text( {bx, by}, " B" );
		Text( {cx, cy}, " C" );
		Pen Color( "blue" );
		Line( {ax, ay}, {bx, by} );// "line a"
		Line( {cx, cy}, {bx, by} );// "line c"
		slopeLineA = (ay - by) / (ax - bx);
		slopeLineC = (cy - by) / (cx - bx);
		// the slope is missing if source line is vertical
		perpSlopeA = If( Is Missing( slopeLineA ),
			0,
			-1 / slopeLineA
		);
		perpSlopeC = If( Is Missing( slopeLineC ),
			0,
			-1 / slopeLineC
		);
		midpointAx = (ax + bx) / 2;
		midpointAy = (ay + by) / 2;
		midpointCx = (cx + bx) / 2;
		midpointCy = (cy + by) / 2;
		Fill Color( "green" );
		Circle( {midpointAx, midpointAy}, .9, "FILL" );
		Circle( {midpointCx, midpointCy}, .9, "FILL" );
		// the perp slope is missing if it is vertical --
		// because source line was horizontal (rise = 0)
		Pen Color( "red" );
		Line Style( "dotted" );
		If( Is Missing( perpSlopeA ),
			pax0 = midpointAx;
			pay0 = midpointAy - 100;
			pax1 = midpointAx;
			pay1 = midpointAy + 100;
		, // else ... find two far-away points and draw line
			pax0 = midpointAx - 100;
			pay0 = midpointAy - 100 * perpSlopeA;
			pax1 = midpointAx + 100;
			pay1 = midpointAy + 100 * perpSlopeA;
		);
		Line( {pax0, pay0}, {pax1, pay1} );
		If( Is Missing( perpSlopeC ),
			pcx0 = midpointCx;
			pcy0 = midpointCy - 100;
			pcx1 = midpointCx;
			pcy1 = midpointCy + 100;
		, // else
			pcx0 = midpointCx - 100;
			pcy0 = midpointCy - 100 * perpSlopeC;
			pcx1 = midpointCx + 100;
			pcy1 = midpointCy + 100 * perpSlopeC;
		);
		Line( {pcx0, pcy0}, {pcx1, pcy1} );
		Line Style( "solid" );
		pensize(2);
		{xc, yc} = lineLineIntersection( pax0, pay0, pax1, pay1, pcx0, pcy0, pcx1, pcy1 );
		Fill Color( "orange" );
		Circle( {xc, yc}, .9, "FILL" );
		Pen Color( "magenta" );
		// choose distance to A, could use B or C too...
		Circle( {xc, yc}, Sqrt( (xc - ax) ^ 2 + (yc - ay) ^ 2 ) );
	);
);

CircleFromThreePoints.jsl