Using Hypothesis Testing to Make Informed Decisions

[#1]

See how to:

• Understand the difference between a Null and an Alternate Hypothesis, the two conditions that we want to investigate
  • Null Hypothesis - generally the status quo, e.g. There is NO DIFFERENCE in the population means from which these two samples were drawn
  • Alternative Hypothesis - the complement of the Null, e.g. There IS A DIFFERENCE in the population means
  • We can also insert Greater Than (or Less Than) instead of No Difference
  • Accepting Alternate Hypothesis is rejecting (or disproving) Null Hypothesis
  • When running tests, we look for proof that the Alternative Hypothesis is within our confidence level, and we can Refute (or Disprove) the Null Hypothesis
  • Caution: If we DO NOT reject the Alt, it DOES NOT mean that the Null is true and perhaps we didn't collect enough data to accept it. 
• Confidence Level is the level of surety involved with the hypotheses
  • Confidence Level needed can depend
    • Often, acceptable Confidence Level for making decisions is 95%.
    • Perhaps if you are looking at life-or-death decisions, you need to be 99.9% confident in the results
  • 95% confidence means  if you run statistical test 100 times, your should be right about 95 times
  • Alpha value is  1 - Confidence/100
• Compare and interpret Confidence Interval on a Mean Value
• Compare Mean to a Target Value
  • Analyze>Distribution and then Test Mean from red triangle
  • Interpret Quanitles, Summary Statistics, Means Test
• Compare two Means
  • Analyze>Distribution and then t-test from red triangle
  • Interpret t-test
• Compare more than Two Means
  • Analyze>Distribution and then Means/ANOVA from red triangle
  • Run Oneway analysis (ANOVA)
  • Interpret Summary of Fit, R-square, Analysis of Variance and Means for one ANOVA
• Hypothesis Testing for Equivalence – Used because when sample means are not different, we still can’t conclude that the population means were the same
  • Alternate Hypothesis is that Population Means are the same, within some specified margin
  • Null Hypothesis is that the Population Means MAY NOT BE the same within the margin.
  • Difference in Population Mean is outside the equivalence interval
  • Employ 2-sided t-tests (TOST)

Note: Q&A is interspersed beginning at ~ Time 20:05.

If you have questions for Jerry, type @JerryFish in your comment.

Resources

• About AICc and BIC 
• Fitting Normal Distribution documentation
• Mastering JMP video and resources for Selecting Proper Sample Size for Your Designed Experiment
• Two Sample Test for Proportions documentation

• SKP Statistics Knowledge Portal 

• STIPS course Statistical Thinking for Industrial Problem Solving

• JMP Wish List for submitting suggestions for enhancing JMP

Compare Mean to Target Value

[carlogarcia]

@JerryFish, Appreciate the slides and lecture you have provided for hypothesis testing.

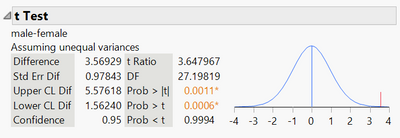
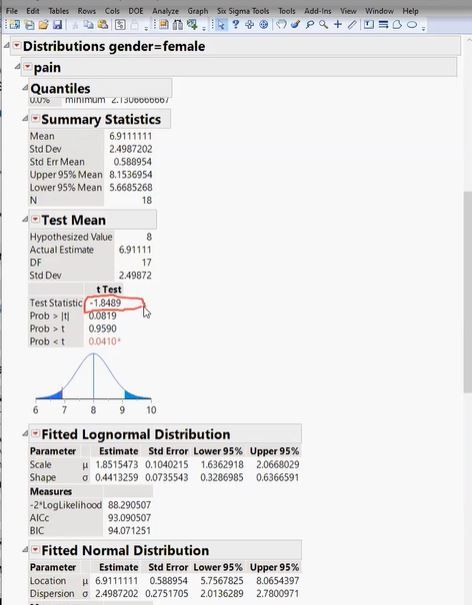
One question I have is that t-test on JMP assumes we have unequal variance:

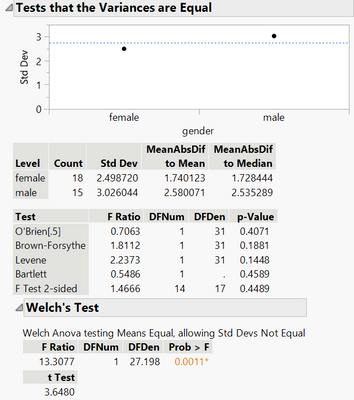
What if our samples are of equal variances, such us this male and female sample.

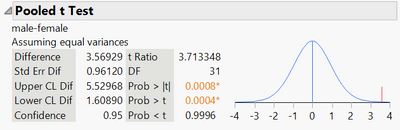
Would the pooled t test a better option?

Thanks.

[JerryFish]

Hi @carlogarcia !  Yes, a pooled t-test would be the better option if you can assume equal variances between the samples. 

As you note, by default JMP assumes unequal variances.  This results in wider confidence intervals (among other things) than for pooled variances, so it is a more conservative evaluation than a pooled t test.

But when you activate the "Means/ANOVA/Pooled t" from the red triangle, the results are indeed pooled.

Of course as you point out, you will want to have confidence that the two group variances are not different, and you get that through the red triangle "Unequal Variances" option.

Thanks for the comments!

[NehaAnilkumar]

Hello @JerryFish ,

How does one estimate the equivalence margin for an equivalence test?

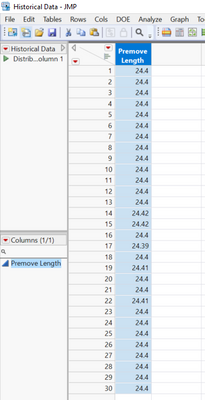
I have a manufacturer who wants to expand manufacturing of a part to a new facility and I want to prove that the process pre move and post move are equivalent.

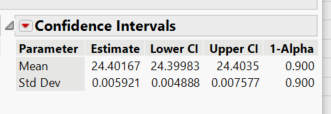
My initial thought was to use pre move data and derive the 90% confidence interval for std deviation and use a value within this range as my margin. But a value between 0.00488-0.007577 seems too small to conduct this study?

Any suggestions?

Thanks

Neha