Mixed Modeling has been the standard for analyzing data with more than one source of random variation (blocking, split-plots, etc.). The Linear Mixed Model (LMM) assumes the response is continuous with no bounds. If your response is a discrete count, binary response or a proportion in terms of y/n, use the Generalized Linear Mixed Model (GLMM).
See how to:
- Underestand the basics of GLMM
- (Video time ~23:40) Understand and hear Q&A from first example - from SAS for Mixed Models (2018), Example 11.5; Beitler & Landis (Biometrics, 1985)
- Multi-location clinical trial
- 8 clinics, two treatments: “CNTL” and “DRUG”
- n_ij patients assigned to treatment i at clinic j
- Response variable y_ij is number of patients with a favorable outcome
- Objective: does “DRUG” increase probability of favorable outcome & if so, how much?
- (Video time ~48:40) Understand and hear Q&A from second example - from SAS for Mixed Models (2018), Example 12.3
- Multi-source, random coefficient regression
- 8 lots
- Amounts X_1=0, X_2=2, X_3=4,… X_6=10 of finishing treatment applied to samples from each lot
- Response variable y_ij is number of aberrant micro-sites on finished product for amount i, lot j – discrete count
- Objectives:
- estimate effect of increasing amount of finishing treatment on aberrant micro-site count
- estimate above via linear regression
- determine amount of finishing treatment required to assure expected aberrant micro-site count ≤ 1
Elizabeth @eclaassen and Jian Cao @jiancao answer questions throughout and discuss plans for enhancing GLMM in future versions of JMP.
Q: Does JMP Pro 17 have the link option to back transform estimates and the confidence intervals?
A: Yes, and we see that in the demo.
Q: What if you find that there is some evidence of over dispersion or under dispersion?
A: I have not run into problems with under dispersion so that's not an issue we are particularly worried about. For over dispersion, often that is a matter of missing a term in the model that we need to include if it still exists after we've gone through the ANOVA process to define our model. Then perhaps it's another distribution that we should be looking at. Or perhaps it's not binomial and it could a zero inflated binomial, or something along those lines, and so we must sort of take that into account.
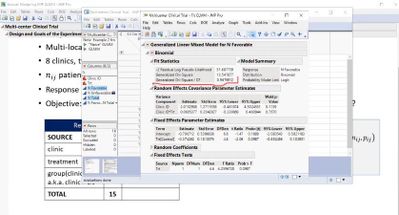 Fit Statistics Chi Square Might Identify Dispersion in ModelFit Statistics Chi Square Might Identify Dispersion in Model
Fit Statistics Chi Square Might Identify Dispersion in ModelFit Statistics Chi Square Might Identify Dispersion in Model
Q: Does GLMM include generalized additive models?
A: No, not currently.
Resources