Underlying principles of structural equation modelling
Created:
Welcome back to my series on structural equation modelling. My first post introduced structural equation modelling and briefly explained where it has been used in the past, as well as where it could be used in the future. In this second post, I aim to explain one of the main underlying concepts used in SEM, typical alternatives and why we employ the concepts we do in SEM. The underlying concept covered in this post is the topic of dimensional reduction techniques and how they are applied in SEM along with the advantages of these methods. I am assuming that the reader has some prior knowledge of dimensional reduction, so the main focus of this post will be on how the techniques are different and what makes certain techniques better for SEM.
Dimensional Reduction
So, what is dimensional reduction, and why do we use it? Dimensional reduction is a technique employed in data science to reduce the data from a high-dimensional space to a low-dimensional space. In other words, we attempt to find a way to represent our data with a smaller number of variables while still retaining the meaningful information from the larger data set.
Dimensional reduction is performed to make a simpler model of the data. Typically, in systems, the variables that have been measured correlate to other underlying causes, and it is usually possible to reduce the model to these underlying causes. There are two main methods to perform dimensional reduction: principal component analysis (PCA) and factor analysis (FA). These two methods are similar but have a few unique differences, which I will explore in this post.
The image below shows one example of how dimensional reduction can be employed with a data set. Say that the data is clustered within the green circles and is initially in three dimensions of X, Y and Z. To reduce the data set, we can attempt to remove some of the less important dimensions to the data such as the Z-axis, which yields the X-Y plot that still contains all our data points. An alternative to this method is to form a Z-Y plot, but by reducing the dimensions of the model in this way, we lose a lot of value data. As you can see from this example, finding the optimal dimensional reduction technique is vital to preserving the important information in the data set, and some data is always lost.
Case Study Background
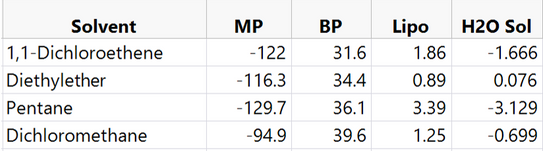
To help with the explanation of this complicated idea, I will use a case study to aid understanding of what it is that we are doing, using a real data set. In this case study, we look at 78 different solvents and various measured property data on each solvent. There are four measured variables for every solvent: Melting point, Boiling point, Lipophilicity and H2O Solubility. The first five solvents and their measured values are reported below:
The objective in this case study is to reduce the dimensionality of our data to make solvent selection simpler for the chemists. To do this, we aim to reduce the four current measurements into two principal components or factors. The ideas of principal components and factors are explored below.
Principal Component Analysis
A principal component is a new variable that is constructed as a linear combination or mixture of the initial variables. The purpose of PCA is to derive a small number of these components that capture as much of the original variability in the data as possible. The end goal is to find the most reduced form of the system that still retains the important information. PCA is particularly useful when there is already a strong correlation between the original variables in the system since this means that there is likely an underlying cause that is correlating the variables.
Principal component analysis is the typical method for dimensional reduction applied in engineering. The primary reason for this is that the measurements taken in engineering almost always have an associated measurement error. By performing PCA, the principal components used to define the system can be found, which include measurement errors as well as variation from other sources.
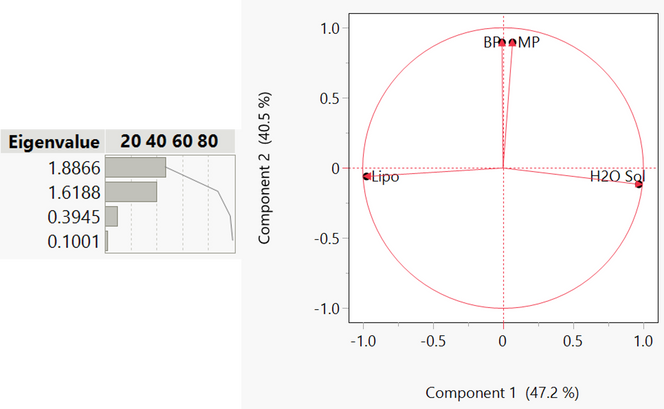
PCA can be performed in the principal component analysis platform in JMP and JMP Pro. This platform is demonstrated here by using the variables for each of our solvents in our case study. To set up the PCA, the four variables must be selected and then added to the platform, and then you simply press “OK”. JMP then automatically computes the principal components of the system and gives the eigenvalues for each component along with a loading plot showing how the original variables correlate to the principal components.
From the Eigenvalues, we can see that principal component 1 is responsible for most of the variation within the data, with principal component 2 accounting for a lesser but still significant portion. The other components, with an Eigenvalue less than 1, each account for less variation than each of the original variables. The loading plot on the right shows how the original variables align with the principal components 1 and 2 (horizontal and vertical axes, respectively). This means that variables that align with each of the principal component axis are correlated with each other via the principal component.
For example, in this case study, we see that the boiling point and melting point are clustered together along the principal component 2 axis; this means that these two variables are highly correlated. From a chemical perspective, we would assume this is the case since the melting points and boiling points of chemicals typically correlate to the forces between molecules. This means that principal component 2 is likely to be the intermolecular attraction between molecules.
Looking at the principal component 1 axis in the same way shows us that lipophilicity and H2O solubility are highly correlated with principal component 1, but inversely correlated to each other since they lie on either side of the axis. Variables at right angles on the graph consequently have no correlation. In a chemical context, we can assume that principal component 1 is likely to be the polarity of the molecules. This is because molecular polarity affects whether a molecule can dissolve in a polar or non-polar solvent; since this is what H2O solubility and lipophilicity are measures of, it is unsurprising that they are highly correlated with this principal component. We also know that a molecule can dissolve regardless of molecular size, meaning that these two measurements should not be correlated with the boiling or melting points, which we see in the loading plot.
Factor Analysis
Factor analysis is very similar to PCA but has some important differences. The main difference in this method compared to PCA comes from the different definition of a factor compared to a principal component.
A principal component is a reduced form of the observed variables that aims to capture as much variation in the data as possible. This means that a principal component isn’t necessarily a “real” variable since it contains the measurement error from the observed variables. Factors in FA however are slightly different. A factor is also called a latent variable, which is an important concept in SEM. A latent variable can be thought of as the underlying reason (or factor) responsible for the observed variables in the system.
As a note, another word for observed variables used in SEM is manifest variables, and so that is how I will refer to these variables from now on. In this way, in FA, manifest variables can be thought of as the measured result of the “real” latent variable, which is unmeasurable in the system.
FA can be performed through the factor analysis platform in JMP Pro. This is done in almost the same way as in the PCA platform, so we perform the same analysis with the same four factors. The only difference in this platform is that there are more customization options related to factor analysis; for simplicity's sake, these options will all be kept as their defaults.
From the platform, we find that there are two main factors. These factors are plotted on the loading plot above to show the percentage of variation that each factor accounts for. Although this plot and the one that was found from the PCA platform look similar, they are not the same.
The key differences can be seen in the amount of variance each factor or principal component accounts for; this is reported on each axis. Another difference is the exact point that each of our variables are plotted on both graphs; this shows that they correlate differently to the factors and principal components. These differences are due to the inherent differences in the way in which we define a factor and a principal component, as explained above. The main example of this is the position of the boiling point variable. In the PCA analysis, it correlates almost exactly to melting point. In the FA analysis, the boiling point and melting point do not correlate as much. This further demonstrates that factor 2 and principal component 2 are two different ideas.
To put this simply in a chemical context, principal component 1 is a measure of ALL the intermolecular interactions, which is why boiling point and melting point are almost identical on that loading plot. On the other hand, on the factor analysis loading plot, we see that the melting and boiling points are now not the same. This is likely because the factor found in the FA is just the Van der Waal’s forces, which is largest force contribution in the intermolecular forces. For various chemical reasons, this means that this factor plays a larger role in the melting point of a substance, but when it comes to the boiling point, other intermolecular forces come into play. These other forces are not accounted for in Factor 1 but are in Principal Component 1, due to the measurement error, which is captured through PCA.
As a conclusion on this idea, we see on each factor’s axis that each factor accounts for less of the variation than the principal components do. This is to be expected since the data used to build the model was empirical and therefore contains measurement error. Consequently, it makes sense that the principal components (which contain measurement error) would account for more of the variation in the original data.
Dimensional Reduction in SEM
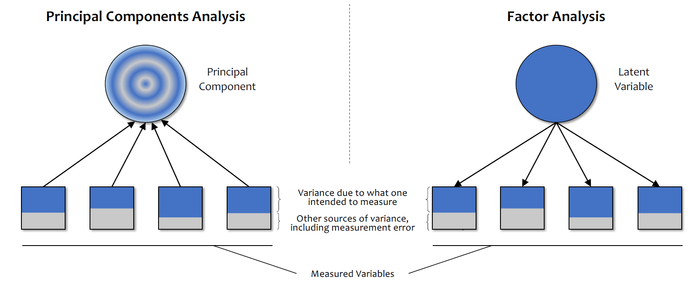
Although PCA and FA are both complicated concepts that deserve books in their own rights to understand them thoroughly, what we can take away from the exploration of these topics is that FA yields latent variables that contain no error, whereas PCA yields principal components that include other sources of error. The second important note is that in FA the latent variable produces the manifest variables, whereas in PCA the principal component is a result of “simplifying” the manifest variables.
Image - Laura Castro-Schilo ABCs of Structural Equation Modeling (2021-EU-45MP-752) - JMP User Community
Both points are visualized in the above diagram, which shows the differences between PCA and FA. In terms of understanding the underlying system FA is the better method. This is because the principal components found in PCA aren’t “real” variables that affect the system. They are just model fitted parameters. This means that PCA is still useful but has far better applications in other fields such as predictive modelling since this may lead to a better fitted model. Consequently, in SEM we employ FA since it allows for a more comprehensive understanding of the underlying causes of the manifest variables in a system. In this way, by using SEM, we can quantify the latent variables through regression on the manifest variables. In fact, this idea makes up the basis of the path diagram, which is a key concept in SEM that I will cover in my next post.
I hope that this has given you an insight into dimensional reduction techniques and why these techniques are and aren’t employed in SEM. An interesting idea within SEM that I will explore in future blog posts is the special case in SEM of confirmatory factor analysis (CFA), which is essentially just a method of employing factor analysis while also setting up a SEM. More on this later.
Comments