Welcome back to another month of structural equation modelling, or SEM. This month, we’re going to take a deeper look into a key feature: path diagrams. A path diagram is the visual way in which we represent the variables in our system when we employ SEM. Path diagrams are composed of a few elements, which we will explore in this post. I will also use JMP Pro to demonstrate how to construct a simple path diagram.
Variables
As I touched on in the previous month’s post, two of the most important types of variables in SEM are manifest variables and latent variables. To reiterate, manifest variables are the variables in the system that we can measure. Some examples in engineering are things like temperature or pressure. In a path diagram, a manifest variable is denoted by the name of the variable in a rectangle, as shown below (ignore the arrows for now – I’ll explain those below).
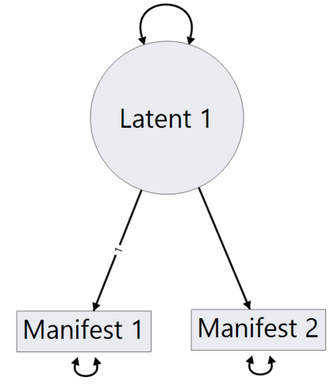
On the other hand, latent variables are variables that cannot be measured directly. Usually, they are ideas or concepts. In traditional social science applications, these latent variables would be ideas like “cognitive ability.” In engineering, defining a latent variable becomes trickier, but there are ideas as to what a latent variable could be. A few examples are the “state of the system,” which is a made-up scale of how well the system is doing. This isn’t something we could measure, but we could infer it from manifest variables, such as the temperature, pressure, or composition of the product.
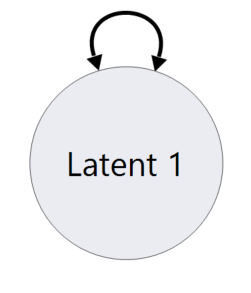
There are other ideas as to what a latent variable could be. For example, as we saw in the last post, a factor in FA contains no other sources of variance, or more specifically, no measurement error. This means that a latent variable could also be used to find the “true value” of a variable that we would usually consider a manifest variable, like temperature. A latent variable is denoted by the name of the variable in a circle, as shown below.
There are two other variable definitions that are important in SEM: exogenous variables and endogenous variables. Exogenous variables are variables whose value is completely independent to the other variables in the system. Conversely, endogenous variables are variables that are dependent on at least one other variable in the system. Typically, the more important definitions are those for the manifest and latent variables, but these definitions are helpful, too.
Covariance and Variance
As we briefly saw above, another key feature of path diagrams are the arrows. The arrows on a path diagram can be single- or double-headed. They can also connect two variables, or just go between the same variable. Essentially, an arrow is a correlation between the variables being connected, and it is up to the designer of the path diagram to choose which variables to connect.
When a double-headed arrow is present, this shows the covariance between two variables (when they affect each other) or the variance within a variable when the double-headed arrow is self-contained within the variable (as seen in the manifest and latent variable examples above).
Loading
Single-headed arrows between variables on path diagrams denote a loading between a manifest and a latent variable. These are used when there is a suspected correlation between two variables. Typically, the significance of the loading values is that for every unit change in the first variable there is a change of the loading amount in the second variable.
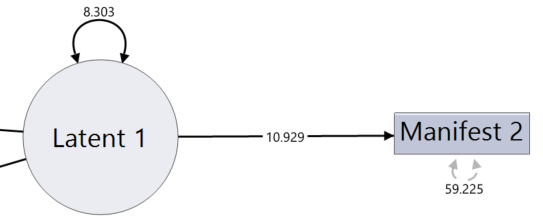
The above picture illustrates how the model fits the loadings to each of the single-headed arrows in the diagram as well as the variance in both variables on the double-headed arrows. There are two types of loadings reported in JMP Pro, the standardized and unstandardized loadings. Unstandardized loadings are the default loadings given, and those are the loadings shown in the above diagram; these loadings reflect the magnitude of the data and therefore are equivalent to the coefficients in a regression model (check out my Discovery Summit presentation on "Exploring Basic Linear Regression Visually Through Structural Equation Modelling" for more details on this).
Standardized coefficients, on the other hand, are simply the correlations between the variables in the path diagram and therefore do not reflect the scale of the original data. Both loading types can be useful, so it’s important to know the difference.
Linear Regression Path Diagram
Now that we have explored the main two features of path diagrams, variables, and the arrows to connect them, we can construct a basic path diagram.
The simplest option in SEM is creating a model only using manifest variables. One example of this is where we use manifest variables connected by a single-headed arrow. By constructing this model, we are recreating linear regression in a visual format with SEM methodology. This can be useful compared to conventional linear regression for several reasons, and if you’re interested in finding out more, I would recommend my Discovery Summit presentation on this topic.

The key benefit to note here is that it is possible to recreate traditional modelling methods in SEM using the path diagrams, therefore making the analysis easier to view by displaying the variables and loadings in a visual format. By analyzing our data in this way, we may uncover relationships that may not be immediately obvious when using traditional analysis methods. One example of this is that we can easily see the contributions of each indirect and direct effect separately when we model our system using SEM. This provides immediate knowledge as to which correlations in our system are the most important to controlling other variables.
I hope that this introduction to path diagrams has given some key insights into why we might want to represent our data in this more visual format. Now that we have established how to create basic path diagrams, next month’s post will focus on how to determine a good path diagram from a bad one, as well as taking a deeper look into some more complicated path diagrams.
You must be a registered user to add a comment. If you've already registered, sign in. Otherwise, register and sign in.