How is the standard deviation calculated for different Shewhart control charts?

[#1]

XR Charts

In an XBar chart that uses the R option, the value for sigma is computed as:

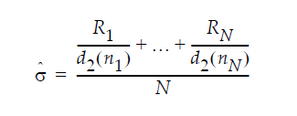
where:

R_i = range of ith subgroup

n_i = sample size of the ith subgroup
d₂(n_i) = expected value of the range of n_i independent normally distributed variables with unit standard deviation
N = number of subgroups for which n_i ≥ 2

XS Charts

In an XBar chart that uses the S option, the value for sigma is computed as:

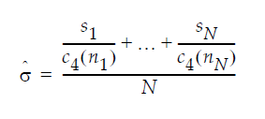
where:

n_i = sample size of ith subgroup
c₄(n_i) = expected value of the standard deviation of n_i independent normally distributed variables with unit standard deviation

N = number of subgroups for which n_i ≥ 2

s_i = sample standard deviation the of ith subgroup

IR Charts

In an IR chart that uses the Moving Range (Average) option, the value for sigma is computed as:

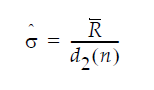
where:

R-bar is the average of the moving ranges

d₂(n) (unbiasing factor) is the expected value of the range of n independent normally distributed variables with unit standard deviation, where n is the value of the Range Span option

In an IR chart that uses the Median Moving Range option, the value for sigma is computed as:

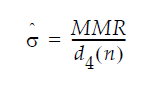
where:

MMR is the median of the non-missing moving ranges
d₄(n) (unbiasing factor) is the median of the range of n independent normally distributed variables with unit standard deviation, where n is the value of the Range Span option

[Previously JMP Note 36576]