How are control limits calculated for the different Shewhart control charts?
This content shows the formulas for control limits for various Shewhart control charts. These formulas use an estimate of sigma. See JMP Note 575376 for information on how sigma is calculated for each chart.
Mean and Range Charts:
You can compute the limits in the following ways:
- as a specified multiple (k) of the standard errors of X-bari and Ri above and below the central line. The default limits are computed with k=3 (these are referred to as 3σ limits).
- as probability limits defined in terms of α, a specified probability that X-bari or Ri exceeds the limits.
The following notation is used for the formulas:
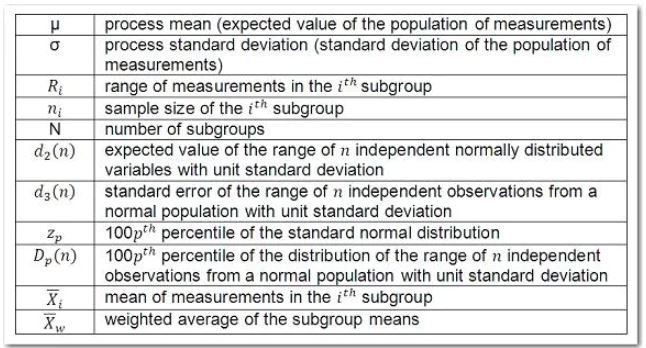
The following tables provide the formulas for the limits:


Mean and Standard Deviation Charts:
You can compute the limits in the following ways:
- as a specified multiple (k) of the standard errors of X-bari and si above and below the central line. The default limits are computed with k=3 (these are referred to as 3σ limits).
- as probability limits defined in terms of α, a specified probability that X-bari or si exceeds the limits.
The following notation is used for the formulas:
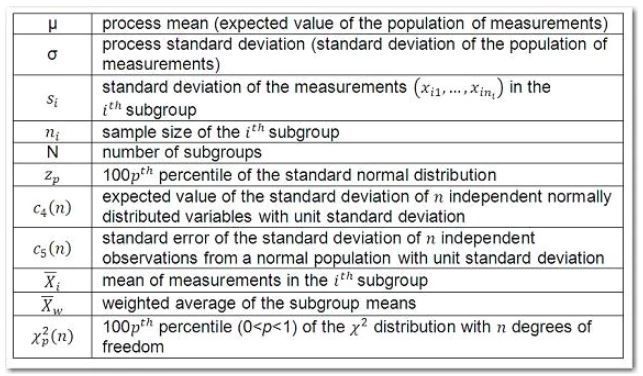
The following tables provide the formulas for the limits:


IR Charts:
You can compute the limits in the following ways:
- as a specified multiple (k) of the standard errors of Xi and Ri above and below the central line. The default limits are computed with k=3 (these are referred to as 3σ limits).
- as probability limits defined in terms of α, a specified probability that Xi or Ri exceeds the limits.
The following notation is used for the formula:
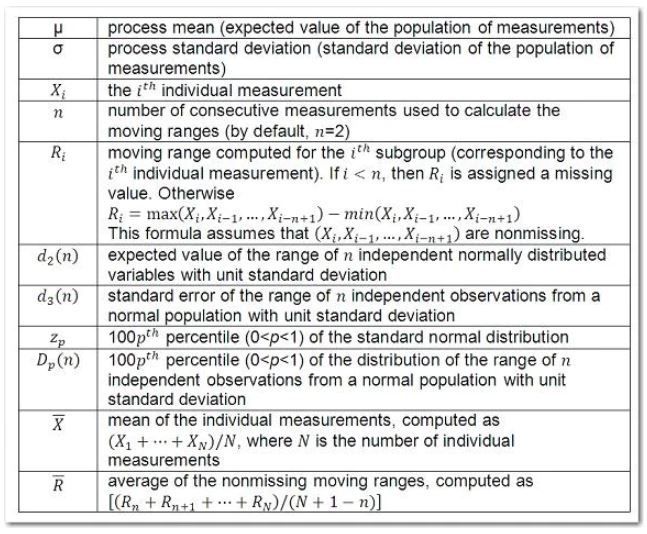
The following tables provide the formulas for the limits:
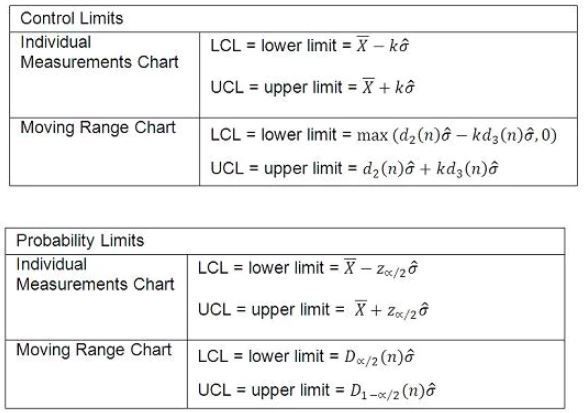
C Charts:
You can compute the limits in the following ways:
- as a specified multiple (k) of the standard error of ci above and below the central line. The default limits are computed with k=3 (these are referred to as 3σ limits).
- as probability limits defined in terms of α, a specified probability that ci exceeds the limits.
The following notation is used for the formula:

The following equations give the formulas for the limits:
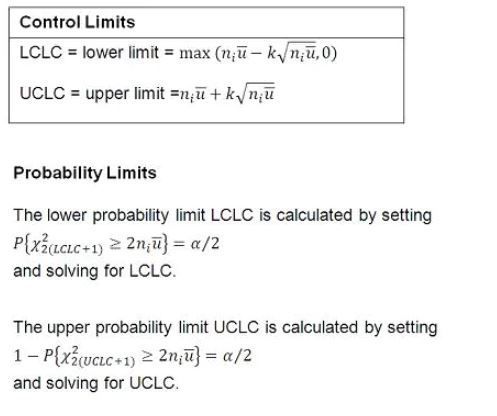
NP Charts:
You can compute the limits in the following ways:
- as a specified multiple (k) of the standard error of Xi above and below the central line. The default limits are computed with k=3 (these are referred to as 3σ limits).
- as probability limits defined in terms of α, a specified probability that Xi exceeds the limits.
The following notation is used for the formula:

The following equations give the formulas for the limits:
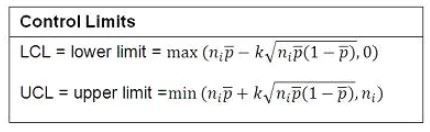

P Charts:
You can compute the limits in the following ways:
- as a specified multiple (k) of the standard error of pi above and below the central line. The default limits are computed with k=3 (these are referred to as 3σ limits).
- as probability limits defined in terms of α, a specified probability that pi exceeds the limits.
The notation for the p chart is the same as the notation for the np chart.
The following equations give the formulas for the limits:
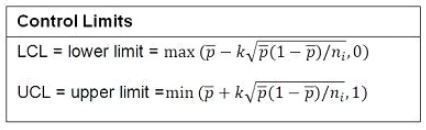

U Charts:
You can compute the limits in the following ways:
- as a specified multiple (k) of the standard error of ui above and below the central line. The default limits are computed with k=3 (these are referred to as 3σ limits).
- as probability limits defined in terms of α, a specified probability that ui exceeds the limits.
The following notation is used for the formula:

The following equations give the formulas for the limits:
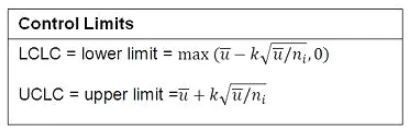

[Previously JMP Note 36484]