Computing an Analysis of Variance with Summary Statistics in JMP® Software
In some instances, an experimenter may want to perform an Analysis of Variance (ANOVA), but only the summary statistics are available. Most statistical programs are designed to compute ANOVA models with the full, complete set of data. However, David A. Larson describes a method to generate surrogate data from the summary statistics which can be used to fit the ANOVA of interest(1). That is, if the analysis is comparing k categories, and only the summary statistics (ni, meani,s2i i= 1, 2, 3,..., k) are available, then data can be generated to perform the desired analysis.
Utilizing Larson's ideas, JMP can perform this type of analysis. The following is an example demonstrating the appropriate steps taken to fit this ANOVA within JMP. If you have only two means to compare, JMP (beginning with version 11) provides an option in the Sample Data Index that can be used. Select Help ► Sample Data (JMP 16 and previous), or Help ► Sample Index (JMP 17 or later). In the Teaching resources section, open Calculators and click on Hypothesis Test for Two Means. Here, choose Summary Statistics radio button option for Choose input method, click OK, and then complete the empty dialog boxes:
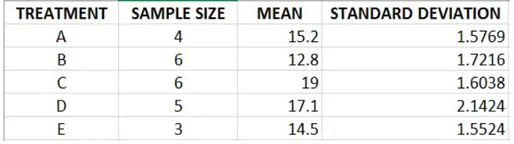
Now, for more than two means, suppose all the information available is presented in the summary statistics below:
The first step is to create a JMP data table with the above data (Table 1).
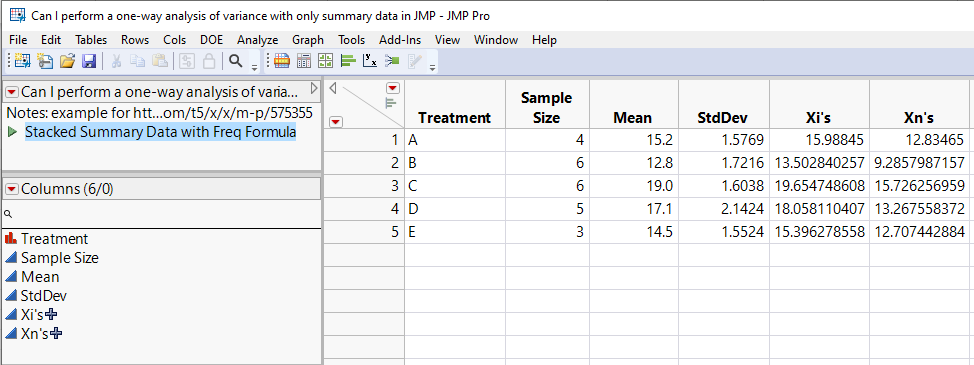
Table 1: The JMP data table
According to Larson, two new columns need to be generated. So, create two columns named "Xi's" and "Xn's" having the Formula Column Property. Then, using JMP's Formula Editor, define these formulas:

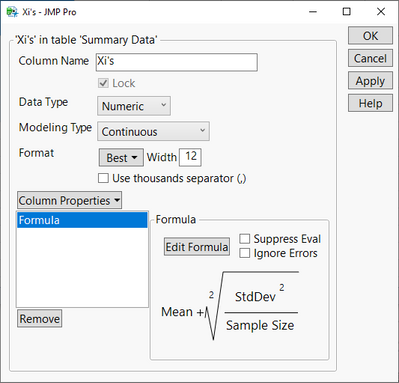
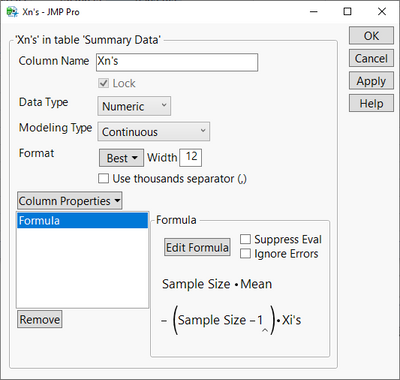
Figure 1: Column Formulas Input into JMP
Once these columns are created, they need to be "stacked." From the Tables menu, select Stack and select the columns "Xi's" and "Xn's" to be stacked, and also, change the name of the Stacked Data Column to "Y" and the Source Label Column to "_ID_" (Figure 2).
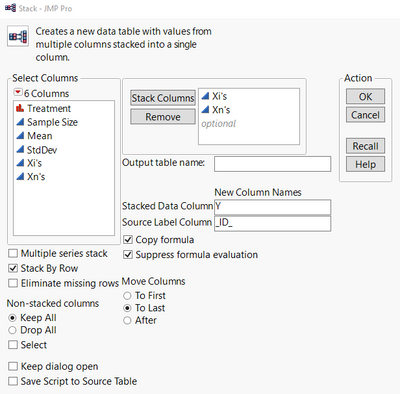
Figure 2: The "Stack" dialog for Summary Data and Xi's and Xn's Columns
The last item necessary to run the model is an appropriate frequency column added to the stacked data table. Using the If function (found in the Formula Editor's Conditional function list), create one more column named "Frequency" with the formula shown in Figure 3 below.
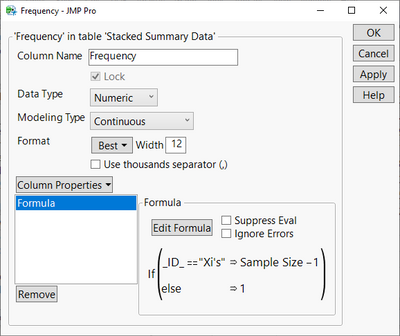
Figure 3: The "if" selection and the formula for "Frequency"
The final data table should appear as shown in Table 2.
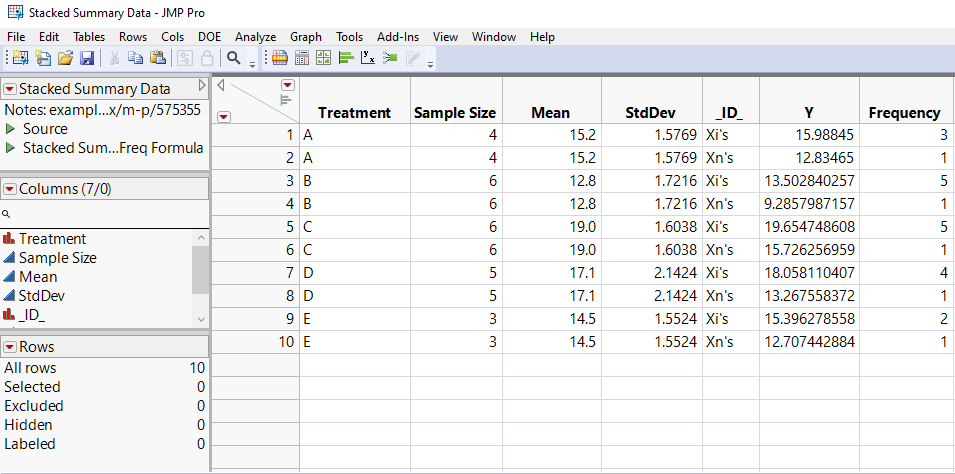
Table 2: Final data table
The surrogate data has been generated so the ANOVA can now be performed. From the Analyze menu, choose Fit Y by X. Specify "Treatment" as "X", "Y" as "Y", and "Frequency" as "Freq," then click OK to run the analysis. The first item seen in the output is a scatterplot of the points. From the Oneway Analysis red triangle menu, click on Means/Anova to produce the resulting output seen in Figure 4.
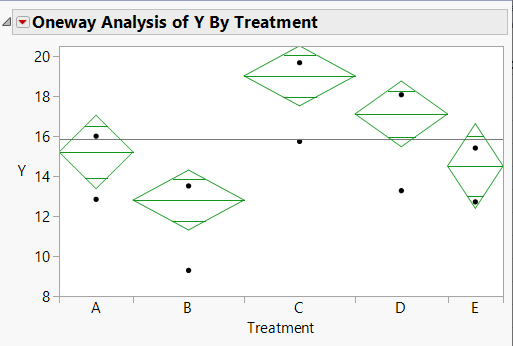
Figure 4: ANOVA results
Oneway ANOVA
Summary of Fit
| Rsquare |
0.690838 |
| Adj Rsquare |
0.625752 |
| Root Mean Square Error |
1.751986 |
| Mean of Response |
15.85833 |
| Observations (or Sum Wgts) |
24 |
Analysis of Variance
| Source |
DF |
Sum of Squares |
Mean Square |
F Ratio |
Prob > F |
| Treatment |
4 |
130.31833 |
32.5796 |
10.6141 |
0.0001 |
| Error |
19 |
58.31965 |
3.0695 |
|
|
| C. Total |
23 |
188.63798 |
|
|
|
Means for Oneway ANOVA
| Level |
Number |
Mean |
Std Error |
Lower 95% |
Upper 95% |
| A |
4 |
15.2000 |
0.8760 |
13.367 |
17.033 |
| B |
6 |
12.8000 |
0.7152 |
11.303 |
14.297 |
| C |
6 |
19.0000 |
0.7152 |
17.503 |
20.497 |
| D |
5 |
17.1000 |
0.7835 |
15.460 |
18.740 |
| E |
3 |
14.5000 |
1.0115 |
12.383 |
16.617 |
Std Error uses a pooled estimate of error variance.
As you see, the means are exactly those that were specified in the initial summary statistics. The standard errors given are estimated using a pooled estimate of the error variance. To compare all results, Table 3 gives the actual data from which the summary data is generated.
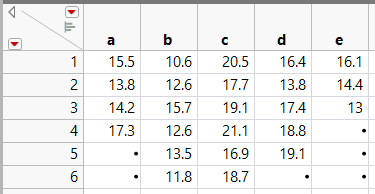
Table 3: Actual data
First the actual data has to be stacked (using Tables ► Stack).
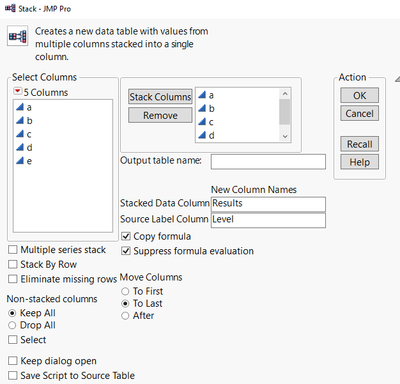
Figure 5. Stack Dialog for Actual Data
The results from an analysis of variance using the actual data align perfectly to the output given with the summary statistics:
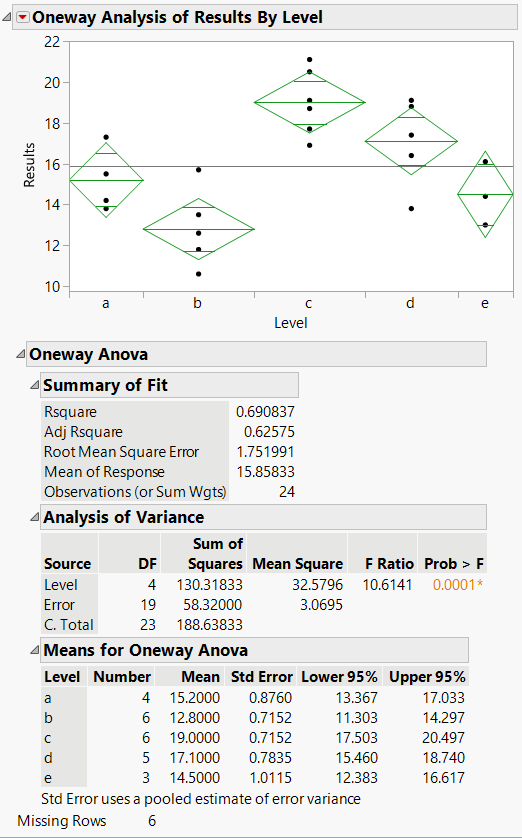
Figure 6. ANOVA output for stacked actual data (matches the analysis output above identically)
In conclusion, if only the summary statistics are available for a Oneway analysis, the method described above can be followed to generate surrogate data in JMP to complete the desired analysis of variance.
REFERENCES
Larson, David A. (1992), "Analysis of Variance With Just Summary Statistics as Input," American Statistician, 46, 151-152.
[Previously JMP Note 35253]