Your 5 most commonly submitted questions about design of experiments (DOE)
Created:
Recently, JMP partnered with the Royal Society of Chemistry and Chemistry World to hold a weeklong series of seminars on experimental design.
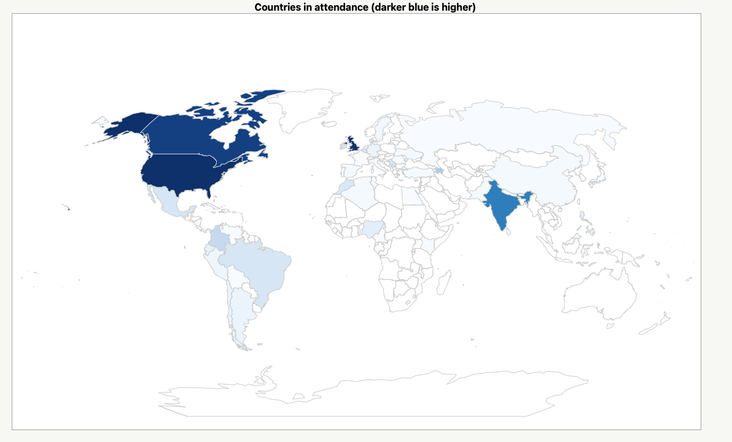
The series was, ostensibly, supposed to be for the eastern and western United States, but, as the attendee map below shows, well – things got a little out of hand on that point.
The seminar series included a panel of JMP experts who would answer questions submitted by the audience. With between 600 and 900 participants in each session, it was challenging to answer all the questions in the flow of the event. And there were a lot of them – on the order of 400 questions in the live session, with even more in the offline environment.
Once the team had recovered (and the joint liniment had done its magic), we got together and looked through the questions for trends to put in the series’ FAQs on the web. In true JMP fashion, we ran these questions through Text Explorer and came up with the top five. Here they are, along with our answers:
Question 1: What is the purpose of center points? When do we need to use them? How many do we need?
OK, we should probably first clarify this: A center point is an experimental treatment that exists in the center of the design space. If you have a three-factor design space, you could map it to a 3D plot, and it would generally look like cube. The center point would sit at the center of the cube, equidistant from all edges, faces, and vertices.
A center point’s primary purpose is to help alert us to curvature (or curvilinear behavior, if you want the $5 word for it) in the data set. A few center points together can also be used as a substitute for replication. That said, you really shouldn’t sweat the question of when to use them. If you focus on model-centric DOE (optimal designs) and other modern DOE strategies like definitive screening designs (DSDs), center points are automatically included when they are necessary. You just have to include model terms that need center points to be studied, and the algorithms take care of the rest. If want to add more center points to study variability (and you’ve already set aside material for a validation set!), then you can add them easily enough. You just have to do a power analysis to figure out the correct number.
Question 2: Do we need to replicate our experiments? Why? Can I use repeated measurements as replicates?
The answer to this depends a lot on the type of experiment you’re doing. If you’re more on the “screening” end of things, replicating is less important because you are looking for gross trends and not so much variability. You might add some center points to get an idea of the variation and do some screening for curvature if you’re not doing a DSD. But that’s about it. If you’re doing model building or refinement, then you probably should do replicates if you have the resources and time.
On the repeated measurements (e.g., running the same factor settings a few times one after the other or obtaining multiple measurements on the outcome of one run of the factor settings), those are not replicated runs. It’s a little confusing because replicates and repeats or repeated measurements sound like they should be the same thing, but there is an important difference in this case.
A replicated run (in the DOE sense) is a randomized repeat of the experiment. Say you were to take a DOE table and put it in a spreadsheet. Then if you were to put a second copy of the complete DOE below it on the same spreadsheet, that still would not be a replicated DOE...yet. Now, if you were to then randomize the row order of the two copies of the DOE, that would be a DOE with replicates.
If you are doing repeated measurements, you can take their average and then use the average as the value for that treatment combination, but they are not the same as replicated runs. The important point is that replication includes randomization and can therefore dilute the effects of lurking variables. Repeated measurements don’t have this property.
Question 3: How many responses can I have in my DOE? How do I work with them?
Adding factors to a DOE increases the cost, in terms of required runs; responses are essentially free. You can measure an unlimited number of response variables to understand how factor changes influence all the responses. When finding optimal process settings using the JMP Prediction Profiler, users can choose a weighting scheme that reflects the relative importance of different responses.
While there aren’t any theoretical limits to the number of responses you have in a DOE, it is to your advantage to define all your responses during the DOE set up. JMP will automatically pass them to the modeling platform after data collection with all the information you provide (upper/lower desirability limits, LOD values, targets, and importances). It also helps make sure you have considered how you are going to gauge success for your DOE and ensure that all your responses can detect differences at the levels you are planning for your factors.
Question 4: How do you know if your factor ranges are appropriate?
One rule of thumb is that if, based on your factor settings, you expect some of your runs to give undesirable results (i.e., end up in the trash), you’re probably right. But you don’t want your ranges to be so broad that you end up with no measurable results at all.
Another way this could be expressed is this advice: Be bold in setting your factor ranges. Set your lows low, and your highs high. There is a great temptation to only look at ranges that make you feel comfortable, because you suspect the optimum is achieved there. Avoid that temptation. The results from the model will be clearer and there will be more precision in the estimates when factor ranges are larger.
If you’re worried that your process will fail to produce usable data in some regions of the design space because of the wide ranges, this concern can often be addressed by defining factor constraints that prohibit runs from being assigned to those areas. Remember, you have the flexibility to use this strategy with optimal designs.
Sometimes experimenters are worried that by setting factor ranges too wide, they may miss an optimum setting that occurs in the middle of the range, due to a curved relationship between a factor and a response. In a custom design, this should be addressed by adding polynomial terms to the desired model, which will cause the generated design to include runs that are set at intermediate factor values between the endpoints.
More generally, you want your experiments to cover a wide enough range to clearly see differences in your settings. You also want your settings to be far enough apart so you can see any inflection points in your curved lines, allowing you to know where “good” and “bad” are. Otherwise, when you optimize, the result will be at the extreme high or low value in your design space. And, you won’t know if you’re close to a place where your system goes out of control.
Question 5: What is the difference between classical design and modern design?
Classical designs are fixed plans that the experimenter must follow, fitting the planned study into their requirements and constraints. These designs were developed before the era of ubiquitous and cheap computing. Modern designs use software algorithms to generate a unique plan for the situation at hand. Modern designs attempt to give the best answer possible for the statistical questions that are posed by the experimenter, while staying within the specified experimental budget.
Modern design is the natural extension of classical design. By running modern DOEs, you don’t lose anything you remember from classical design, but you gain a great deal of flexibility. Fundamentally, modern designs are model-centric in that they make the design fit a model made up of terms defined by the user. As a user, you are deciding what you want to learn in the experiment by selecting the model. Classical designs are design-centric in that they define the design, and the user is expected to make their questions fit into that predefined design. In many cases modern and classical approaches will lead to the same design because the classical designs are optimal for fitting standard models. Modern designs enable you to find the optimal design in situations where classical approaches would not work, like when you have an irregularly shaped factor space that you need to explore.
The adventure continues
And that’s it. When looking at the results, it was interesting to see how frequently these questions came up. It reminded me of something many of my teachers said: “Ask the question, because it’s very likely that others also have it but are too shy to ask.”
Anyway, do you think we missed one? Are there other burning questions that you have about DOE? Go ahead and put them in the comments, and we’ll see what we can do about getting them answered. Until then, happy experimenting!
Comments