Introduction
I was far too old when I learned the details surrounding the time value of money. Of course, I knew that interest compounds investments, and that – to paraphrase Einstein – you're either the type that's paying compound interest or the type that's earning it. I recently did a year-end checkup on my retirement funds and asked myself two questions:
- Will I ever have enough saved to retire?
- Can I use JMP to do the retirement checkup?
It turns out that the Yes that answered the second question gave me a good answer for the first question. Read on to learn about using JMP for financial analysis.
Building the tool in JMP
I figured the easiest way to do a retirement checkup was to make a model to forecast a future account balance, based on interest rates, number of years until retirement, and annual contributions. As I thought about it, I realized I could probably let JMP do most of the work for me with existing tools: the Custom Designer, Financial formulas already built in to JMP, and a combination of Profiler, Simulator, and the Design Space Profiler.
The first step is making the data table. To do this, I used the Custom Profiler to generate just the limits of what the internet says are valid assumptions about rates of return and median balances. I did some educated guessing to come up with a range of savings rates, including employer matches. (See the image below for how to set up the Custom Designer and make the initial data table.) Since the Balance response will be a formula, I chose a main effects model, which will help the Profiler know appropriate limits later on.
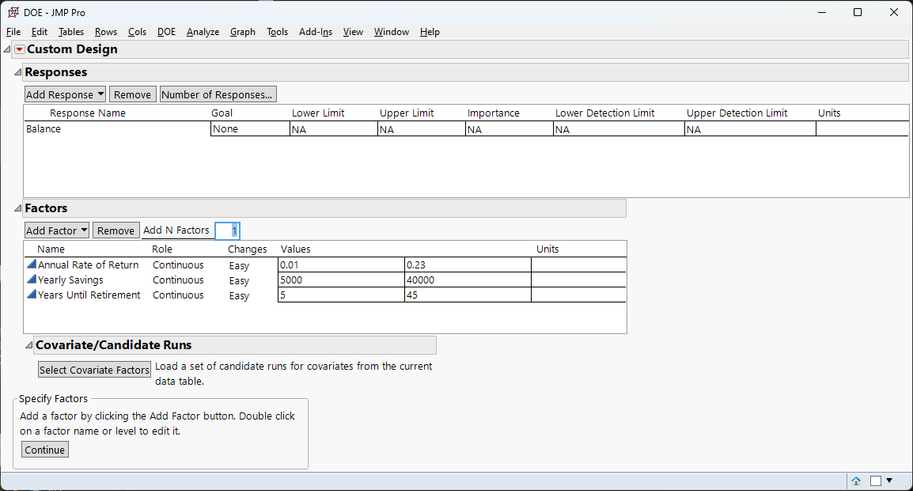
The next step is to make the Future Value calculation work. To do this, I first created a table variable and entered how much I have currently saved in retirement. For the sake of my privacy, I'll use a made-up persona, Mike, who is currently 45 and has $100,000 saved, which is the median for this age group.
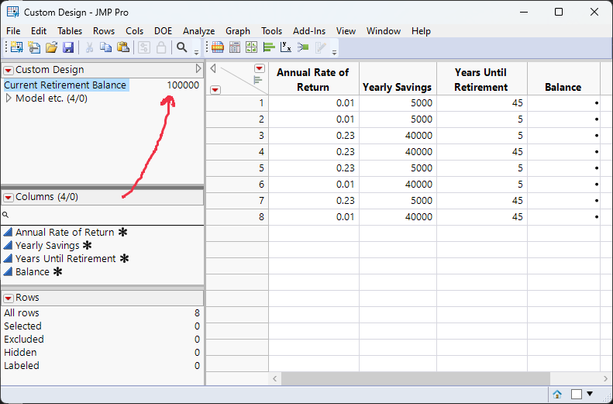
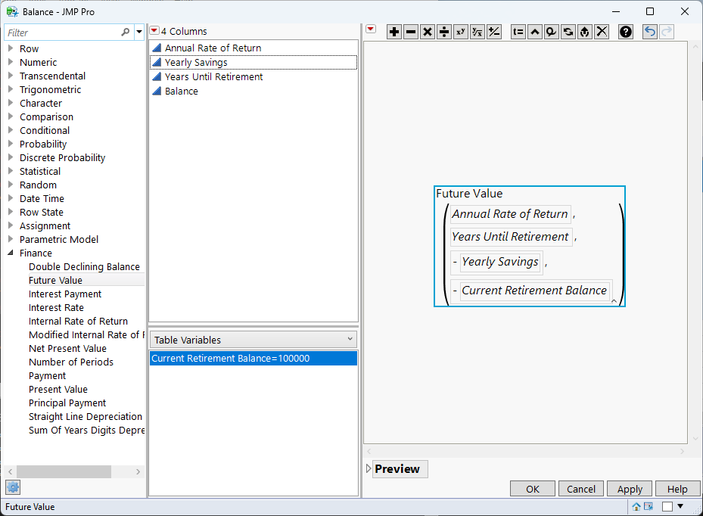
After this, it's time to create the formula in the Balance column. This is really easy, since it's already included with JMP. However, two parts might not be obvious:
- The Future Value function can accept four parameters, with the fourth being the current amount.
- Note that I added some minus signs in the formula. While it's simpler for me to think in terms of all positive numbers, TVM calculations assume that payments and initial values are negative. Think of it as relinquishing money to the savings account, if that helps.
Finally, it's just a matter of using the Graph...Profiler and some red triangle options to get an interactive tool to predict retirement. The Design Space Profiler is useful here because it shows that Mike, who is 45 and only has $100,000 saved so far, has about a 70% chance of having $1.5 million saved if he works between 15 and 25 more years, saving between $20K and $30K each year, assuming his returns each year vary between 1% and 23%.
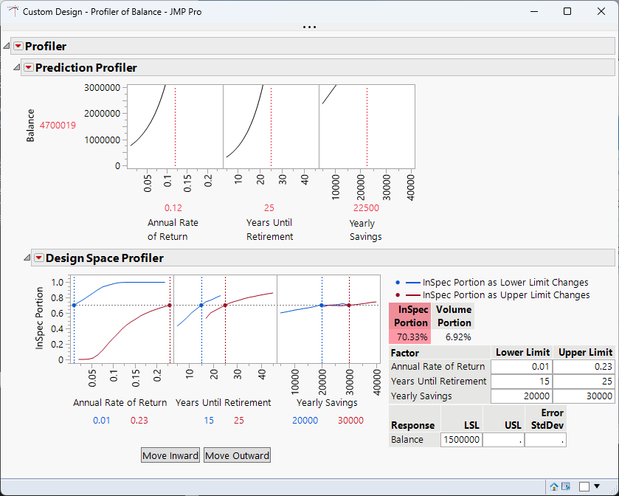
With the script for this tool saved to the data table, it's simple enough to adjust the Current Balance table variable and run other scenarios. For example, Chris, who is 57 and currently has $150K saved for retirement, only has about a 4% chance of having $1.5 million saved for retirement in the next five to 10 years, even after putting quite a bit into savings.
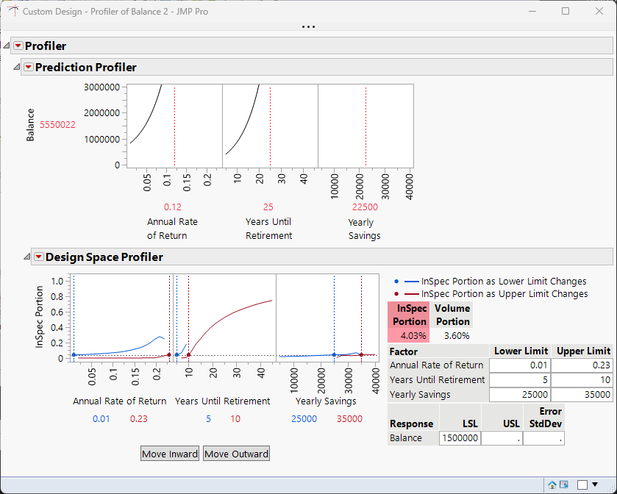
On the other hand, Pat, who is 24 and already has $45K saved, has an almost 84% chance of having $2 million saved by age 55-56, a situation that just serves to illustrate the lesson that starting early is important.
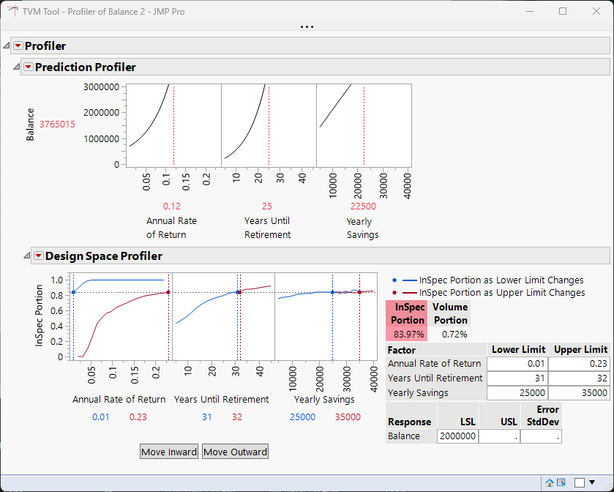
Other uses
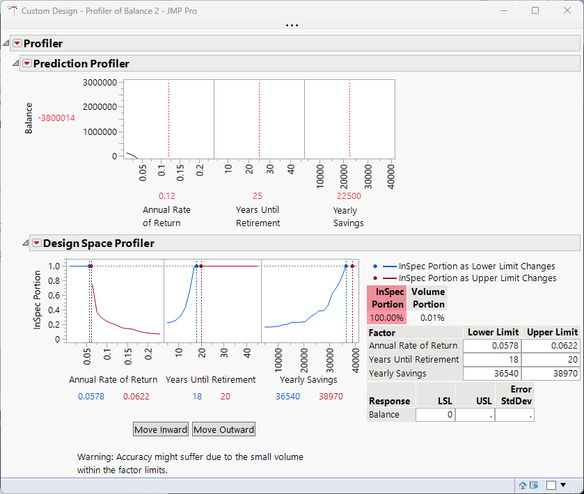
The tool can be used other ways, as well. Changing the Current Balance to a negative number can allow for forecasting of how long it will take to pay off a mortgage. As an example, a mortgage of $400K at an interest rate of 6% would require annual payments of about $36K to pay it off in about 18 years. In this case, it might be better to have labeled my columns differently, but the formula works just fine.
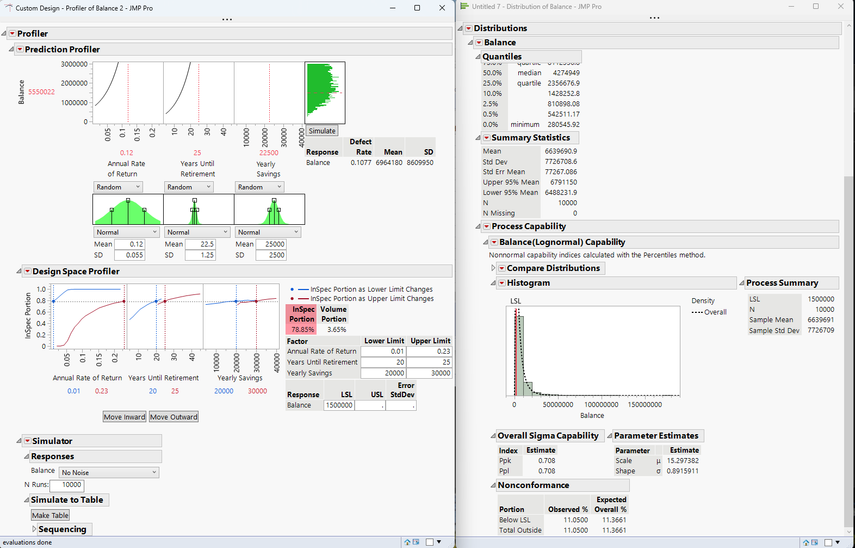
Finally, if I really want to dive into the details, I can simulate all this to a table and look at the results in the Distribution platform.
Conclusion
My personal conclusion is that it's important to start saving early for retirement. Of course, having a tool to visualize this makes it much easier to explain to my kids. I've attached a copy of the data table with the tool attached. What other uses can you see for time value of money calculations?