JMP Blog
A blog for anyone curious about data visualization, design of experiments, statistics, predictive modeling, and more- JMP User Community
- :
- Blogs
- :
- JMP Blog
- :
- The same, similar, or different?
- Subscribe to RSS Feed
- Mark as New
- Mark as Read
- Bookmark
- Subscribe
- Printer Friendly Page
- Report Inappropriate Content
Comparing things is common in our everyday lives. If you are missing an ingredient for a recipe, you might have something else on hand that could serve as a good substitute. For comparison decisions that require data, you might wonder if an older machine is performing comparably to a new machine in a lab or factory. Is it time to repair or replace the older machine or is its performance “good enough” to continue using it? And how do we quantify what “good enough” means in this context?
Conventionally, comparing two things requires the cumbersome, and often counterintuitive, use of hypothesis testing. However, simply rejecting or failing to reject the null hypothesis may not sufficiently address the question we hope to answer. So, how can we more effectively determine if two things are the same, similar, or different? The answer can be found by using the probability of agreement (PoA) methodology for evaluating practical equivalence, which is one of Nathaniel Stevens’ areas of expertise. He was our most recent guest on Statistically Speaking, and we were delighted to learn more about this powerful and flexible framework.
Nathaniel is an Assistant Professor of Statistics in the Department of Statistics and Actuarial Science at the University of Waterloo. He has won several awards, most recently the 2023 American Society of Quality Feigenbaum Medal and the 2021 Søren Bisgaard Award for his work in Bayesian probability of agreement.
Since we had more questions than time to answer them, Nathaniel has kindly agreed to share more of his expertise here.
What are the limitations of the PoA framework?
The framework relies heavily on the equivalence threshold 𝛅. As such, this is something that needs to be determined thoughtfully. In certain settings, this may be difficult to do. And without careful consideration, this could be unscrupulously chosen for a desired outcome. It’s therefore imperative that that 𝛅 be chosen in recognition of the problem context.
Is PoA equivalent to changing the significance level to 0.1 (for example) instead of the 0.05 threshold used in a traditional hypothesis test?
No, the relationship between the PoA analysis and hypothesis testing is not quite that straightforward. Although many incarnations of the PoA exist, to help build intuition for what it quantifies and how it relates to other measures of evidence, let’s consider an illustrative example where we simply wish to determine whether a parameter θ lies within the interval [-𝛅, 𝛅].
This may be done (for example) with second generation p-values[1], an equivalence test[2], interval-based methods[3], [4] or the frequentist probability of agreement[5]. All of these approaches, by different methods, seek to characterize the location and dispersion of the sampling distribution of θ-hat specifically in relation to the interval [-𝛅, 𝛅]. Interval-based methods tend to check whether a confidence interval for θ lies entirely outside or within [-𝛅, 𝛅]. Second generation p-values measure the extent to which such statistical intervals overlap [-𝛅, 𝛅]. The p-values associated with two one-sided tests (TOST) in aggregate measure the proportion of the sampling distribution of θ-hat that lies outside of [-𝛅, 𝛅]. And the frequentist PoA measures the proportion of this distribution that lies inside [-𝛅, 𝛅]. All of these methods, in similar though subtly different ways, quantify evidence in favor of the statement θ ∈ [-𝛅, 𝛅].
Is PoA being taught in schools? When did it start?
To my knowledge, PoA is not yet taught in courses. The idea is fairly straightforward, and I expect I’m not the first to consider it. So, I can’t say for certain when the first instance of this idea was implemented. However, the framework my collaborators and I have begun to build began roughly in 2015.
This is a problem more generally with the teaching of any methodology that explicitly accounts for practical equivalence. Such methodologies (e.g., equivalence tests) are rarely taught in introductory courses. Broad acceptance of this class of methods requires a paradigm shift in pedagogy, which will hopefully be brought about by the paradigm shift that we are experiencing in the statistics discipline with respect to statistical vs. practical significance.
What does “HDI” mean?
HDI is an acronym for “highest density interval.” Generally speaking, an HDI is the subset of a univariate distribution’s support that has highest density[6]. The idea is used commonly in Bayesian inference as a particular type of posterior credible interval. For instance, consider the posterior distribution for a parameter θ, and consider an interval [L, U] that contains 95% of the distribution and hence, contains θ with probability 0.95. Such an interval is not unique. The 95% HDI is the shortest interval that contains θ with probability 0.95.
How do you define the term “heteroscedasticity”?
Generally speaking, heteroscedasticity refers to nonconstant variance. In contrast, homoscedasticity refers to constant variance. In the measurement system comparison context, heteroscedasticity is relevant because a measurement system’s variability (i.e., its repeatability) may not be a fixed constant; it may instead be a function of the item you are measuring. For instance, the measurements may become more/less variable if the item being measured is large/small. However, the distinction between homoscedasticity and heteroscedasticity is relevant more broadly. For example, inference within ordinary least squares regression is predicated on a constant variance assumption, which gives rise to the need for variance stabilizing transformations (e.g., the log-transformation) in the presence of heteroscedasticity.
Are there any special considerations that must be made if assessing agreement/non-inferiority based on ratios?
The PoA (and related comparative probability metrics) can be defined either with respect to the additive difference C1 - C2 or the relative difference C1/C2. Aside from being careful to correctly specify the distribution of C1/C2, the only other key consideration when working with ratios is how to define practical equivalence and hence, the region of practical equivalence (or non-inferiority).
In this case, determining whether C1/C2 is practically different from 1 is of interest. Thus, it is sensible to define the region of practical equivalence as [(1 + δ)-1, 1 + δ] where here 𝛅 is chosen in recognition of the fact that a percent increase of 100𝛅% is the smallest that is practically important. Such an interval is symmetric around 1 on the relative scale and is invariant to the (potentially arbitrary) labeling of Group 1 vs. Group 2. The PoA is then defined as
How do you define the equivalence limit for the Cox model? How do you use the equivalence limit in the Cox model?
The PoA has not been developed for use with the Cox proportional hazard model specifically, but it certainly could be. Defining the equivalence margin in this case would require thinking about how different (on the additive or relative scale) must two hazard functions be before it becomes practically relevant. This equivalence margin may be a constant, or it may depend on the covariates in the model. There is nuance and flexibility in this regard. I urge someone to pursue this methodological development; it could be highly useful.
Do you know of climate modelers using these methods to evaluate their models?
Not specifically, no. The closest thing I’m aware of is a recent paper by Ledwith et al. (2023)[7] that uses the probability of agreement to validate computational models more generally. But I expect methodology such as this could be useful for climate model evaluation.
We are grateful to Nathaniel for taking the time to share more of his thoughts on this flexible and powerful concept. If you missed the livestream, check out the on-demand episode of this Statistically Speaking.
[1] https://www.tandfonline.com/doi/full/10.1080/00031305.2018.1537893
[2] https://www.routledge.com/Testing-Statistical-Hypotheses-of-Equivalence-and-Noninferiority/Wellek/p/...
[3] https://www.tandfonline.com/doi/full/10.1080/00031305.2018.1564697
[4] https://psycnet.apa.org/record/2012-18082-001
[5] The Bayesian PoA would be useful here as well, but to narrow the scope of the discussion, I’ll focus on the frequentist version.
[6] Highest density regions (HDR) are the multivariate analog.
[7] https://asmedigitalcollection.asme.org/verification/article/8/1/011003/1156689/Probabilities-of-Agre...
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us


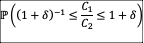
You must be a registered user to add a comment. If you've already registered, sign in. Otherwise, register and sign in.