The power and flexibility of Generalized Linear Mixed Models (GLMMs)

[#1]

Many new capabilities have been added to JMP 17 and JMP Pro 17, several of which were featured at our recent Discovery Summit Americas event. With GLMMs now in JMP Pro 17, we were delighted to feature one of the world’s foremost GLMMs experts in our recent episode of Statistically Speaking. Professor Emeritus Walter Stroup of the University of Nebraska, Fellow of the American Statistical Association, and co-author and author of several books including, Generalized Linear Mixed Models: Modern Concepts, Methods, & Applications gave the opening plenary. We were also delighted to feature one of his former students, Dr. Elizabeth Claassen, who gave the closing plenary. She is now a Senior Research Statistician Developer at JMP where she is lead developer on the new GLMM capabilities.  She has co-authored several books including JMP for Mixed Models (you can access the first chapter of this book for free). 

We had so many good questions from the audience that we didn’t have time to answer, and Walt and Elizabeth have kindly elaborated on some of the issues raised and provide answers to the remainder of the questions below. Elizabeth addressed the JMP-specific questions, and both collaborated on the others that follow.

A Note from Elizabeth

As I was finishing the first example with the binomial data, I meant to show the profiler again in the GLMM fit to compare the confidence interval to the one in the LMM. I was so excited to get to the second example, I guess! So, let’s take a look at them both here.

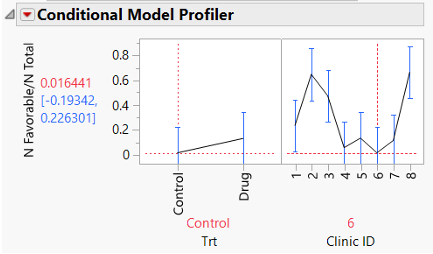
First, here’s the Profiler from the first, LMM, fit of the data.

As noted in the presentation, the confidence interval for the predicted probability of a favorable outcome on the Control treatment at Clinic 6 is (-0.193, 0.226). That negative probability estimate is infeasible because probabilities must be between 0 and 1!

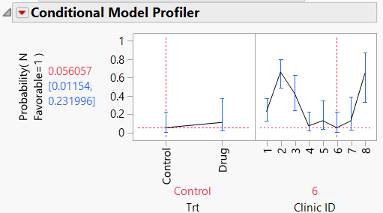
How does the GLMM fit do? Let’s add the same conditional profiler and see.

Here the predicted probability for the Control treatment at clinic 6 is 0.056, a bit higher than the LMM, but not a lot. The confidence interval, though, is now within a reasonable range for a probability (0.012, 0.232). Because we’re modeling the logit, when we use the inverse link function to obtain the probability, we’re guaranteed the resulting probability is between 0 and 1. We no longer have to worry about CIs that don’t “make sense”. The same would be true with the Poisson distribution and the log link; we’re guaranteed a predicted rate greater than 0.

But your CI contains one, so why would you report it as significant, rather just say a trend?

In the clinical trial example when we analyzed the data appropriately with the binomial distribution, we ended up with a fixed effect test p-value of 0.0987. Depending on the context, we might consider this significant at the a=0.10 level. The confidence interval for the odds ratio is reported with the default 95% confidence. This corresponds to an a=0.05 level and results in a wider interval than a 90% confidence interval. This 95% interval does contain 1, which would typically be considered non-significant. Thus, it looks like a mismatch between significance and “a trend”.

We can change the alpha-level used in the report to a=0.10, and then we can see what happens. The default alpha is an option in the Model Dialog red triangle menu.

With the alpha level changed, we see that our p-value is the same as before, 0.0987, and now the corresponding 90% CI for the odds ratio no longer contains 1. Now the alpha level for the CI “matches” with comparing the reported p-value as significant at the a=0.10.

Would I ultimately use the a=0.10 in this clinical context? Likely not, particularly if this was a late-stage trial. I referenced that level simply to demonstrate. But there are contexts (perhaps in early drug development) where a more relaxed significance level is reasonable. There are also contexts where a more stringent significance level is required!

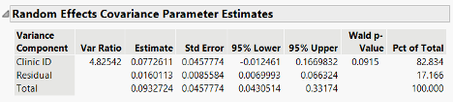
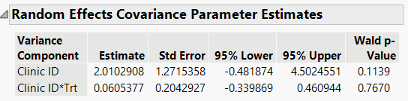
Why not show the ‘Pct of Total’ variance component in the GLMM?

This is a great question and highlights another difference between the Gaussian LMM and the GLMM.

In the LMM we include the percent of the total variance in the Random Effects Covariance Parameter Estimates table, because in a LMM it is truly a partition of variability of the response.

In the GLMM, however, the variance components are now not partitioning the variability of the response in the same way because the distribution is not Gaussian. For this example, the Clinic ID variance is an estimate of the variability of the logits, or log odds, between clinics. The Clinic ID * Trt variance is an estimate of the variability of the log odds *ratios*. Because the variability isn’t on the same scale, we don’t have a total in the same manner as in the LMM to then have a percent of total to report. It doesn’t make sense in the GLMM context.

Any guidelines for having sufficient sample size? 

Important question. Sufficient sample size – and a study design that is well-planned for accuracy and efficiency – allows you to get the most out of your GLMM analysis. Chapter 16 in my [Walt’s] GLMM textbook (Generalized Linear Mixed Models – Modern Concepts, Methods and Applications, 2013, CRC Press) describes GLMM-based methods for determining power and sample size and has several examples showing how to implement these methods. GLMM-based methods are extensions of Gaussian mixed model power and sample size procedures described in Chapter 4 of SAS for Mixed Models, 2018 edition. This chapter also describes design-selection approaches you can use in conjunction with mixed model power calculations. You can use these approaches with GLMMs as well as Gaussian mixed models.

Do you think the JMP implementation of GLMMs will make more people aware of and use this relatively new class of models?  Maybe it will make teaching the concepts easier?

Yes. A little history. Following the introduction of SAS PROC MIXED in the early 1990s, there was a strong demand for mixed model workshops and short courses – from professional meetings, ASA chapters, private industry, and government entities such as the FDA, CDC, Agricultural Research Service, etc. I belonged to two organizations, University Statisticians of Southern Experiment Stations (USSES) and the North Central Coordinating Committee (NCCC), whose members together represented the applied statistics entities at most of the Land Grant universities in the US. Those universities with degree programs in statistics modified their linear model curriculum to include mixed models and modified their statistical methods courses for graduate students in disciplines considered “consumers of statistical methods” to include mixed model methods relevant to the needs of these consumers. A similar thing happened coinciding with the introduction of PROC GLIMMIX.

From a 2022 perspective, “linear model” means GLMM – classical ANOVA and regression models, generalized linear models, Gaussian – a.k.a. linear – mixed models are all special cases of the GLMM. The University of Nebraska’s Statistics degree program modified its statistical methods and linear model core curriculum accordingly, as did several other USSES or NCCC participant universities. Many biostatistics programs at medical colleges did so as well.

With this history in mind, the JMP implementation of GLMMs should have an impact in two ways: on degree programs in statistics and data science, and on awareness among JMP users who already have degrees and work in academia, government, or the private sector. Undergraduate degree programs in data science are proliferating. Students in these programs need to have some awareness of GLMMs and how to work with them. JMP is ideal software to use as a teaching tool in this context. For those who received degrees without a GLMM component, continuing education is a must. The implementation of GLMMs in JMP should help stimulate demand. Examples of GLMM implementation using JMP would be an integral part of continuing education workshops and short courses.  

Does dealing with the 'residual' aspect of data when using GLMM make it a little dated in utility compared with 'neural networks' though?

There is a time and place for different modeling procedures. Neural networks are amazingly flexible with regards to the type of data (both responses and predictors) used. They can be very good at predicting when there are a lot of predictors or with unstructured or observational data. However, in settings where some form of study design is possible (designed experiments, survey designs, retrospective studies that can be organized as pseudo-experiments), GLMMs are better suited to estimating or testing factor or treatment effects or providing an explanation to the researcher as to “best” factor settings, etc. Galit Shmueli lays out these issues in her wonderful paper “To Explain or to Predict?” (Shmueli, G. 2010. To explain or to predict?, Statistical Science 25, no. 3, 289–310; we were also delighted to feature her in an episode of Analytically Speaking).

Expanding on this point, with the GLMM we are typically working with structured data, perhaps from a designed experiment, a planned survey, or a retrospective pseudo-experiment. There are defined experimental units (or sample survey equivalents thereof) for various sources of variation (blocks, whole- and split-plots, units of observation), and usually defined treatments, such as the control and drug or the finishing treatment in our examples. The researchers typically have specific goals, e.g. to measure a treatment effect or to find the best treatment level, and need to explain the model and decisions they reach. In these cases, a formal linear model is the better choice of procedure, so we must “deal” with the ‘residual’ by fitting the appropriate distribution with all the necessary fixed and random terms.

We thank Walt and Elizabeth for taking the time to share more of their knowledge of GLMMs and some relatively recent and fascinating history in statistics!  We hope you will watch the on-demand version of this episode of Statistically Speaking and see how you may avoid bias and get more value from your data with the use of GLMMs.