JMP Blog
A blog for anyone curious about data visualization, design of experiments, statistics, predictive modeling, and more- JMP User Community
- :
- Blogs
- :
- JMP Blog
- :
- The QbD Column: Split-plot experiments
- Subscribe to RSS Feed
- Mark as New
- Mark as Read
- Bookmark
- Subscribe
- Printer Friendly Page
- Report Inappropriate Content
Editor's note: This post is by @ronkenett, @david_s and Benny Yoskovich of the KPA Group. It is part of a series of blog posts called The QbD Column. For more information on the authors, click the authors' community names above.



Split-plot experiments are experiments with hard-to-change factors that are difficult to randomize and can only be applied at the block level. Once the level of a hard-to-change factor is set, we can run experiments with several other factors keeping that level fixed.
To illustrate the idea, we refer in this blog post to an example from a pre-clinical research QbD (Quality by Design) experiment. As mentioned in the first post in this series, QbD is about product, process and clinical understanding. Here, we focus on deriving clinical understanding by applying experimental design methods.
The experiment compared, on animal models, several methods for the treatment of severe chronic skin irritations[1]. Each treatment involved an orally administered antibiotic along with a cream that is applied topically to the affected site. There were two types of antibiotics, and the cream was tested at four different concentrations of the active ingredient and three timing strategies.
The experiment was run using four experimental animals, each of which had eight sites located on their backs from the neck down. Thus, the sites are “blocked” by animal. For each animal, we can randomly decide which sites should be treated with which concentration by timing option. The antibiotics are different. They are taken orally, so each animal could get just one antibiotic, and it would then apply to all the sites on that animal.
The analysis included a number of outcomes, and the most important were those that tracked the size of the irritated area over time, as a fraction of the initial size at that site. The primary CQA (Critical Quality Attribute) summarizing the improvement over time is the area under the curve[2] (AUC), and that is the response that we will analyze in this blog post. The AUC is an overall measure of the rate of healing, with low (high) values when healing is rapid (slow).
For more details on split-plot experiments, a great source is the introductory paper by Jones and Nachtsheim.
Why is split-plot structure important?
In the topical cream treatment study, the animals form experimental blocks. The basic reason for considering blocks in the data analysis is that we expect results from different sites on the same animal to be similar to one another, but different from those for sites on other animals. We take advantage of this property when we compare timing and concentration. Those comparisons are at the “within animal” level, which neutralizes the inter-animal variation and thus improves precision. For the antibiotics, the differences between animals will affect our comparison. The fact that we think of each animal as a block means that we do expect to see such differences. We need to take this into account both in designing the experiment and in analyzing the results.
What are whole plots and sub plots?
We use the term “whole plots” to refer to the block-level units and “sub plots” to refer to the units that are nested within each whole plot. In the example above, the animals serve as whole plots and the sites as sub plots. The terminology goes back to Sir R.A. Fisher, the pioneer of the statistical design of experiments. Fisher worked at an agricultural research station in Rothamsted, UK, in the early 20th century. Typical experiments at this station involved comparing types of crops, planting times, and schedules of irrigation and fertilization.
Fisher observed that some of these factors could be applied only to large plots of land, whereas others could be applied at a much finer spatial resolution. So “whole plots” to Fisher were the large pieces of land, and “sub plots” were the small pieces that made up a whole plot. Some experiments have more than two such levels. Nowadays, we continue to use these terms, even though split-plotting affects many kinds of experiments, not just field trials in agriculture, and the “whole units” and “sub units” usually are not plots of land. In the QbD context, they consist of animal models, like in the example used here, batches of material or setup of production processes.
When does split-plotting occur?
There are many possible sources of split-plot structure in an experiment. Sometimes, as above, we have “repeat measurements,” but at different conditions, of the same experimental subject. Sometimes the experiment involves several factors that are difficult to set to varying experimental levels, such as a column or bioreactor temperature. In that case, it is common to set the hard-to-change factors to one level and leave them at that level for several consecutive observations, in which the other factors are varied. This leads to a split-plot experiment, with a new whole plot each time the hard-to-change factor(s) are set to new levels. Sometimes a production process naturally leads to this sort of nesting. For example, consider an experiment to improve production of proteins for a biological drug. The process begins by growing cells in a medium; then the cells are transferred to wells in a plate where they produce protein. An experiment might include some factors that affect the growth phase and others that affect only protein production. Dividing the cells in a flask among several different wells makes it possible to test the production factors at a split-plot level.
How do I design a split-plot experiment?
The Custom Design Tool in JMP makes it easy to create a split-plot design. First, enter the factors in your experiment. The split-plot structure is specified using the column labeled “Changes” in the factor table. The possible entries there are “easy,” “hard” and “very hard,” corresponding to three levels of nesting among the factors. Factors that can be assigned at the individual observation level are declared as “easy” (the default setting). Factors that can be applied only to blocks of observations are declared as “hard.” There may be a third level consisting of factors that can be applied only to “blocks of blocks,” and these factors are labeled as “very hard.” Figure 1 shows the factor table for our experiment. Antibiotic is the hard-to-change factor because it is applied to the animal, not the individual sites. Timing and concentration are numerical factors, as the company wished to get information for comparing all the levels under consideration, without the need to extrapolate by a regression model. So we decided to declare all the factors as categorical. Note that a concentration of 0 means applying a base cream with no addition of the compound being tested. 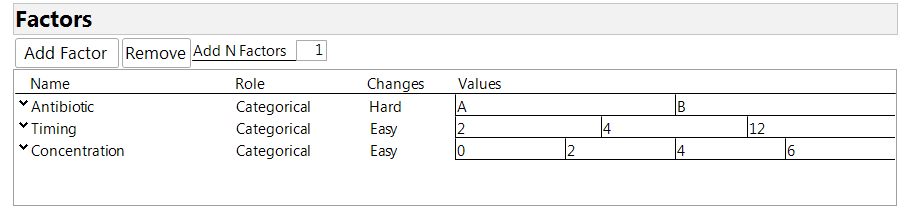
Figure 1: Factor definition for the experiment
The next step is to specify any special constraints. For example, some factor combinations may be impossible to test, or there might be some inequality constraints that limit the factor space. Then you need to declare which model terms you want to estimate, including main effects and interactions. In our experiment, the company wanted to estimate the main effects of the three factors. They wanted information on the two-factor interactions but did not consider it essential; however, the experiment is large enough to permit us to estimate all these terms. If there were fewer runs, we could indicate the “desired but not crucial” status by clicking on the estimability entry for these terms and choosing the “if possible” option. See Figure 2. 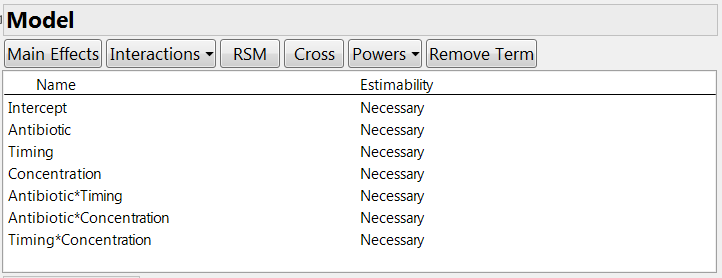
Figure 2: Model definition for the experiment
We are then asked to specify the number of whole plots, i.e., the number of animals available. For our study, there were four animals. Finally, we need to specify the number of runs. The Custom Design tool recommends a default sample size, tells us the minimum possible size and allows us to specify a size. In our experiment, it was possible to stage eight sites on each animal, for a total of 32 runs. Clicking on the “Make Design” button generates the design shown in Table 1. There are four whole plots with each antibiotic assigned to two of them. There are 12 combinations of timing and concentration, but only eight sites on each animal. So it is important to make an efficient choice of which of these treatment combinations will be assigned to each site. Moreover, there is no textbook solution for this allocation problem. This is a setting where the algorithmic approach in JMP is extremely helpful. 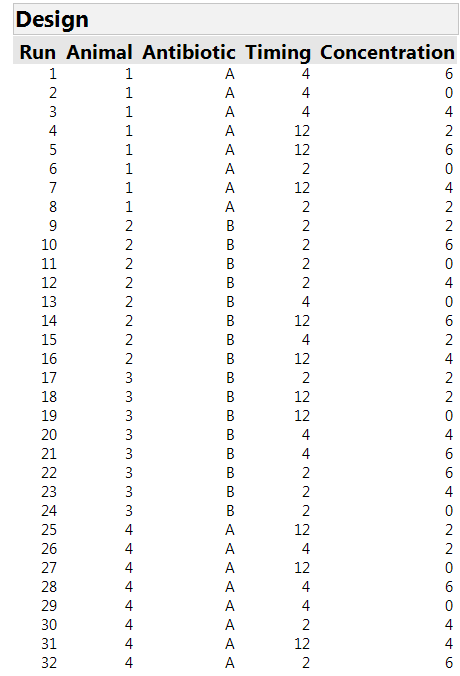
Table 1: The 32-run design for three factors in four whole plots of eight runs each. The factor “antibiotic” can only be applied at the “whole plot” level.
The design found by JMP uses the two-hour time scheme for 12 sites and each of the other schemes for 10 sites. Each concentration is used eight times. Each timing by concentration option is used either two or three times. (Note that we would need 36 runs to have equal repetition of the combinations, but the experiment has only 32 sites.) The design automatically includes a Whole Plots column – in our experiment, this tells us which animal is studied, so we changed the name of the column to "Animal."
How does a split-plot experiment affect power?
The power analysis in Table 2 is instructive. We see that the power for the timing and concentration factors is much higher than for the antibiotic. The higher power is because we are able to compare levels of these factors “within animal,” thus removing any variability between animals. For the antibiotics, on the other hand, the comparison is affected by the variation between animals, so that the relevant sample size is actually four (the number of animals) and not 32 (the number of sites). 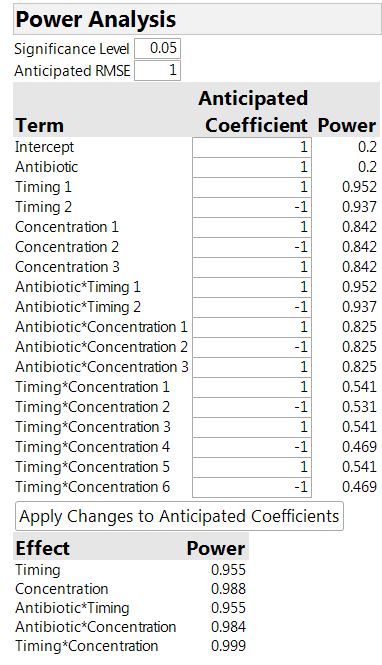
Table 2: Power analysis for the 32-run design
It is important to realize that the power analysis must make some assumptions. These include the size of the factor effects (the Anticipated Coefficients) and the magnitude of the variances. The entry for RMSE in the table is for the site-to-site variation. There is also an assumption about the size of the “between animal” variation to the “within animal” variation. The default assumption is that they are roughly the same size. If you thought that most of the variation was between animals, the default should be changed to a number greater than 1. To do so, click on the red triangle next to Custom Design, select the Advanced Options link, and then the Split-Plot Variance Ratio link.
How do I analyze a split-plot experiment?
The analysis follows the same general structure as for other designed experiments; see the earlier blog posts in this series. The major difference is that we need to add the factor Animal to the design as a “random effect.” It is this random effect term that tells JMP that the experiment is split-plot. Use the Fit Model link under Analyze. If you do this from the design table, the list of model terms will automatically include the random effect. If you access the data differently, then you will need to add Animal to the list of model effects and to declare it as a random effect by highlighting the term and clicking on the “Attributes” triangle next to the list of model terms. The first option there is “Random Effects.”
What happened in the skin irritation experiment?
We analyze the results on AUC. Effective treatment combinations will have low values of AUC. Table 3 shows tests assessing whether the factors have significant effects. There is a clear effect associated with concentration (p-value=0.002). The effect for timing has a p-value of 0.076, so there is an indication of an effect, but much weaker than for concentration. The F-statistic for comparing the two antibiotics is larger than the one for timing. However, it has a p-value of 0.078, close to the one for timing. The reason is that the antibiotic comparison is at the “whole plot” level and so has more uncertainty, and much lower power, than the comparisons of timing strategies and concentrations. 
Table 3: Effect tests
None of the interactions is strong. So concentration is clearly the dominant factor. Table 4 and Figure 3 summarize the estimated effect of concentration on AUC. There is a clear relationship, with higher concentration leading to lower AUC, hence faster healing. 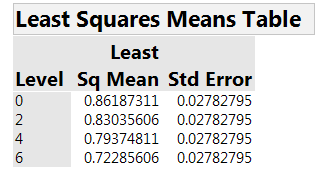
Table 4: Estimated mean AUC for the four concentrations
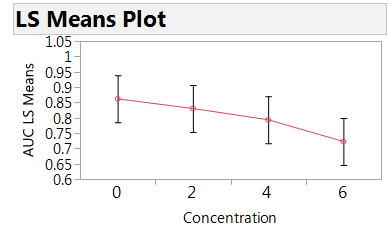
Figure 3: Plot of the estimated mean AUC by concentration
The analysis includes a random effect for “Animal,” reflecting the team’s belief that part of the variation is at the “inter-animal” level. Table 5 shows estimates of the “within animal” (residual) and the “between animal” variances. The Var Component column lists the estimated variance components: 0.0029 at the “within animal” level and 0.0010 at the “between animal” level. The first column gives the between animal variance as a fraction of the “within animal” variance, estimated to be about 0.34 for our experiment. 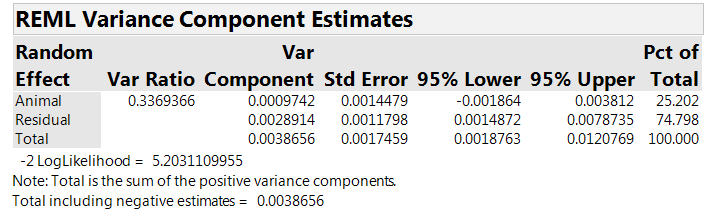
Table 5: The estimated variance components
What are the take-home messages?
The topical cream study provided valuable information that the cream is more effective at higher concentrations. The use of multiple sites per animal permitted “within animal” comparisons of the concentrations and timing, so that the positive effect of increasing concentration could be discovered with a small number of animals. The “between animal” variation was only about 1/3 as large as the “within animal variation.” This was a surprise, as we had expected that there would be substantial inter-animal variation. Of course, the estimate of inter-animal variation is based on a very small sample, and thus quite variable, so we will still be careful to take account of split-plot structure in future experiments like this one. Consequently, factors that must be administered by animal, rather than by site, will be detectable only if they have very strong effects or if the number of animals is increased.
Coming attractions
The next post in this series will look at the application of QbD to design analytic methods using Fractional Factorial and Definitive Screening Designs.
References
[1] For more information on testing topical dermatological agents, see the FDA “Guidance for Industry” document at http://www.fda.gov/ohrms/dockets/ac/00/backgrd/3661b1c.pdf [2] In the example, we use data normalized to [0,1] after dividing all by the largest AUC. [3] Jones, B. and Nachtsheim, C. (2009). Split-Plot Designs: What, Why, and How, Journal of Quality Technology, 41(4), pp. 340-361.
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us

You must be a registered user to add a comment. If you've already registered, sign in. Otherwise, register and sign in.