Ever been confused when someone said that an
ANOVA is the same thing as
regression? Or felt resentment toward the math teacher who told you that you'd use slope-intercept form one day? Well, get ready to send a huge box of chocolate to your old algebra teacher, because Y = mx + b is back, baby. Or rather, it never left.
Now that the ANOVA is in your analysis toolbelt, let's do a quick recap. What’s really under the hood of an ANOVA is a linear equation: Y = mx + b. If I want to see whether people over 40 years old have more dental fillings than those under 40, I'd use this equation:

In an ANOVA, the variable (X) is what we call a “dummy variable.” It can only take on the values of 0 or 1 (you either are or are not under 40 years old). 0/1 coding of groups is called indicator-variable coding, one of a few types of coding schemes — like effect coding — that you may see in JMP.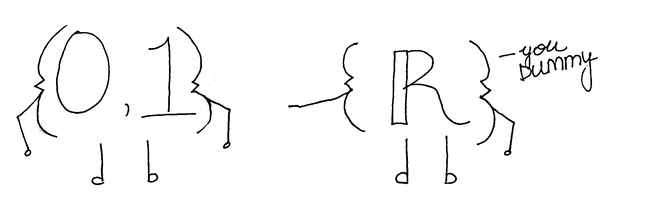 If someone is under 40, we give them a 0 for X, and if they are over 40, we give them a 1. Age is the difference between the mean number of fillings for each group.
If someone is under 40, we give them a 0 for X, and if they are over 40, we give them a 1. Age is the difference between the mean number of fillings for each group. 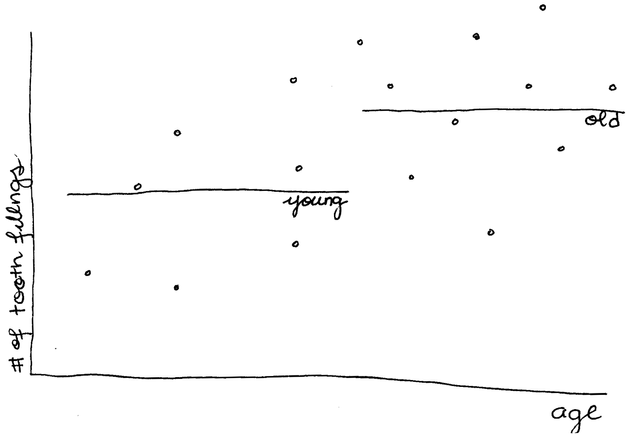
Regression uses the same exact equation, but it allows the coefficient to be any real number, just like in middle school! The m (or slope) in the case of a regression means “we expect Y to change this much for every time we increase X by 1 unit.”
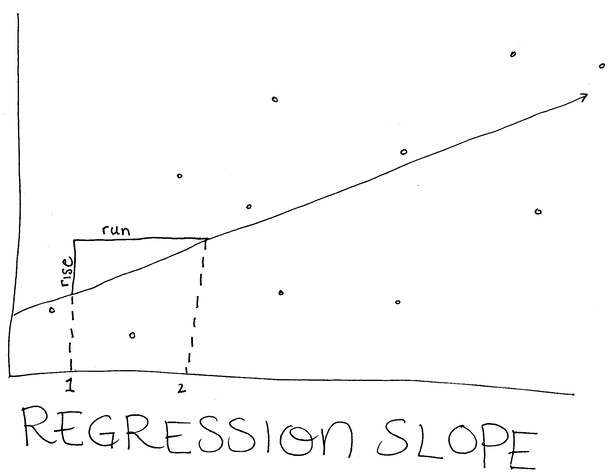
The m (or slope) in an ANOVA is the same, but you’re only able to increase by 1 unit since you can only have a 0 or 1 for X (our expected change in Y is the difference between the means).
 In a regression, instead of testing whether the means of two or more groups are significantly different, we are testing whether the slope of a line is significantly different from zero (we’re still doing this in an ANOVA, but the “slope” in an ANOVA is the difference between the two means).
In a regression, instead of testing whether the means of two or more groups are significantly different, we are testing whether the slope of a line is significantly different from zero (we’re still doing this in an ANOVA, but the “slope” in an ANOVA is the difference between the two means).
Significance tests for regressions are exactly the same as for ANOVAs. I’m going to look at the relationship between number of unique words in Rhianna songs by year released [1] (there are only so many times you can say “work” in one song).
Sums of Squares Total (SST)
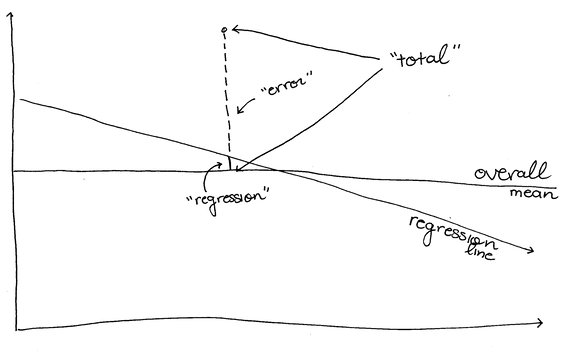
First, we need to calculate the total variance in the data. This is done the same way as in an ANOVA — we take the sum of the squared differences between each point and the mean. [2]
Sums of Squares Regression (SSR)
Second, we calculate the variance due to “group” like we did in the ANOVA, but we don’t have groups. Instead we have a line that predicts values for Y based on values of X so we calculate the Sums of Squares Regression (SSR). For every value of X, we subtract the predicted value for X from the mean of all of the values (the grand mean).

Sums of Squares Error (SSE)
Just like before, the SST = SSR - SSE which means we could calculate Sums of Squares Error by taking SST and subtracting SSR but, just for fun, let’s do it the long way. 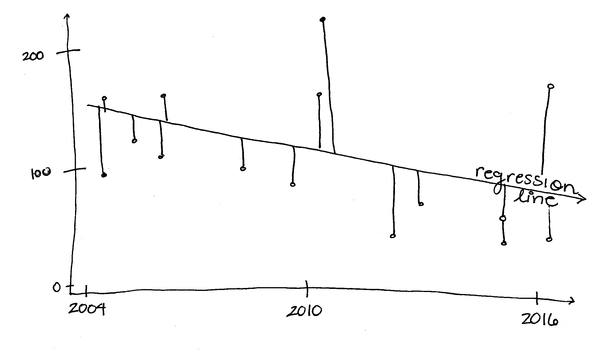
All we do is take the actual value at X minus the predicted value at X (in ANOVA, we do this too, but our expected values in the ANOVA are group means). Remember, again, that Regression (like ANOVA) takes the total amount of variance, puts it into different groups, and compares them. Here, we are comparing variance due to regression and variance due to error. Together, these make up the total amount of variance; if it's not due to regression, it's chalked up to error.
The F test
Now that we have all of our Sums of Squares, all that’s left is the F test!
Just like in an ANOVA, we take the amount of variance due to regression and error and divide them by their respective degrees of freedom [3] to get the Mean Squares (MS) for each of our terms.
Our F-statistic is calculated by dividing MS for regression by the MS for Error. In essence, this tells us the ratio of variability that the regression accounts for the variability that we didn't model — or error variance. If we only account for as much variability as random error, we don't think our effect is significant.
To do this in JMP, open BadGirlRiRi.jmp (attached).

Using the Analyze>Fit Y by X, Drag Unique Words over to the Y box, and Year to the X box.

Click Ok and the output window will pop up. Using the red triangle under Bivariate Fit to select Fit Line.
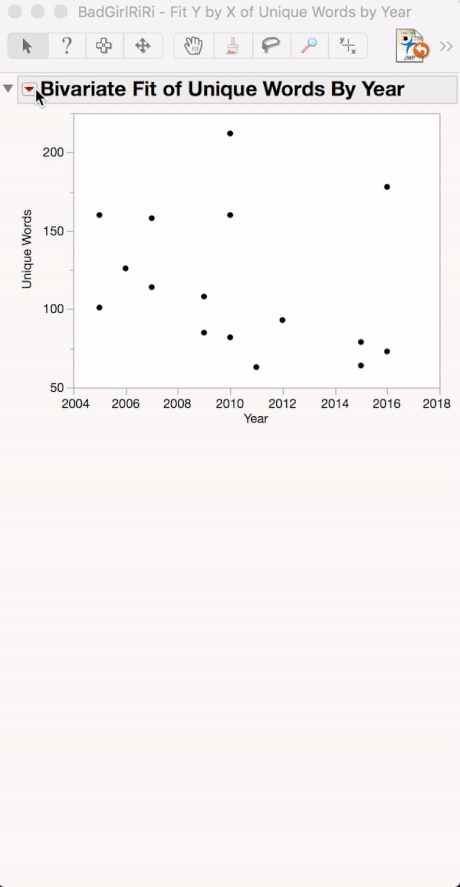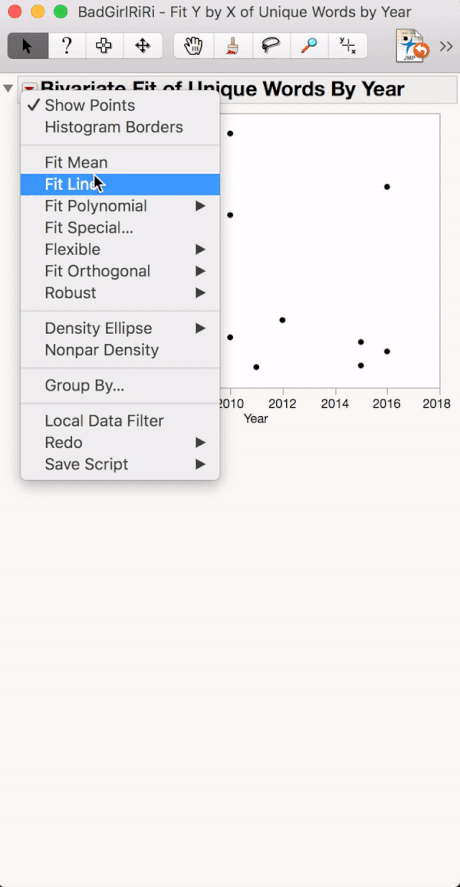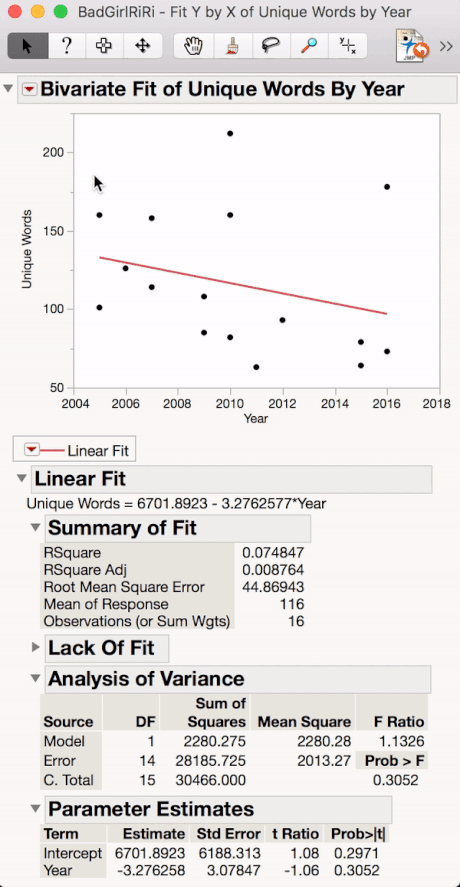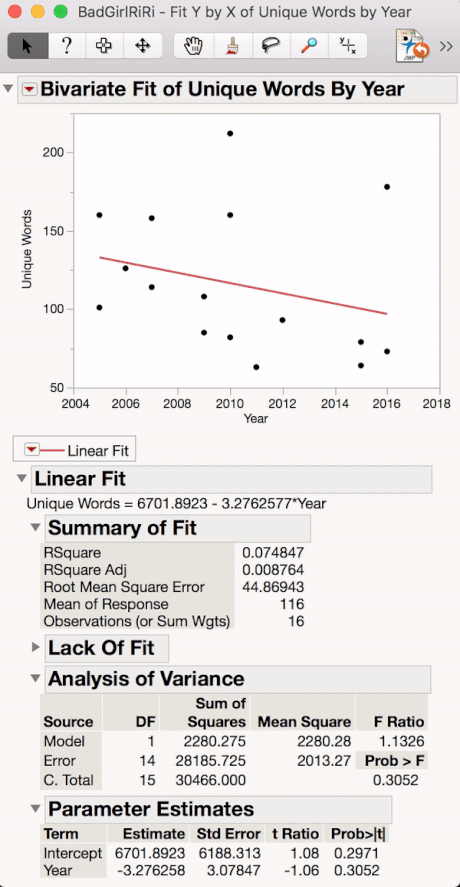
Notice the Analysis of Variance table displays our Sums of Squares, Degrees of Freedom (DF), Mean Squares, and our F test. Since our F is relatively close to 1, and our p-value is way higher than 0.05, we do not have evidence that there is a statistically significant relationship between number of unique words in Rhianna songs and year, but I'm keeping an eye on you, Riri....
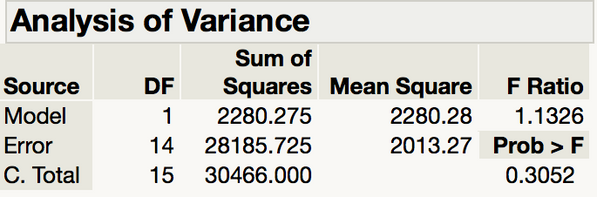 ANOVA table from Fit Line
ANOVA table from Fit Line
So that is linear regression in a nutshell, and why the ANOVA is just a special case of regression — I'm afraid it’s linear turtles…I mean models…all the way down.
Have a topic you want covered?
Feel to reach out on Twitter @chelseaparlett! The preferred form of request is "What the heck is _________?"
Notes
[1] For the Jupyter Notebook that extracts the Rhianna data, see this repository.
[2] If you want to follow along with the calculations, see this sheet.
[3] Why do we do this? Degrees of Freedom essentially represent "new" information. We want to get the most "bang" for our information "buck," i.e., we want the most variability explained for the fewest degrees of freedom. Dividing the total variability by the degrees of freedom gives us the amount of "per degree of freedom" variability. It's not fair to compare the amount of variability a factor with 89 pieces of information accounts for to the amount of variability a factor with one piece of information accounts for. For a review of degrees of freedom, see this article.