關於SPC在產品良率管制方面已有很多成熟的方法。如根據產品不良率分析的P/NP圖,根據產品不良點數的U/C圖,或者是產品不良率的分佈形式符合正態分佈,直接按照連續型資料處理的方法,如圖1所示。
U of # defects
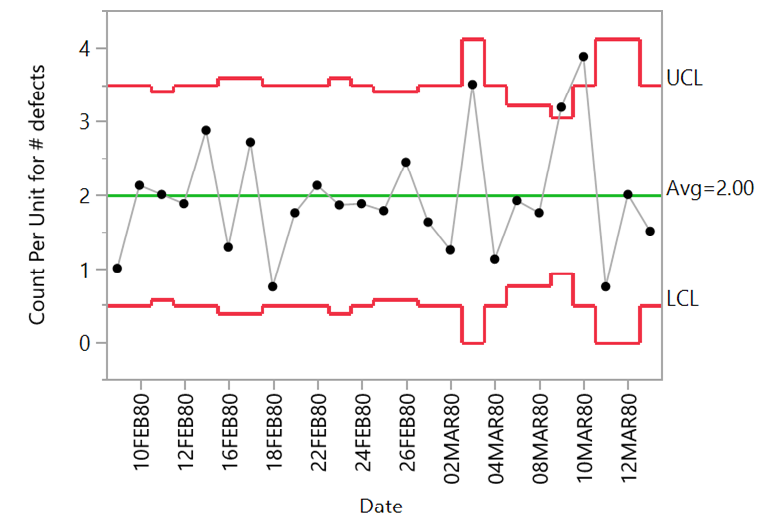
P of # defective
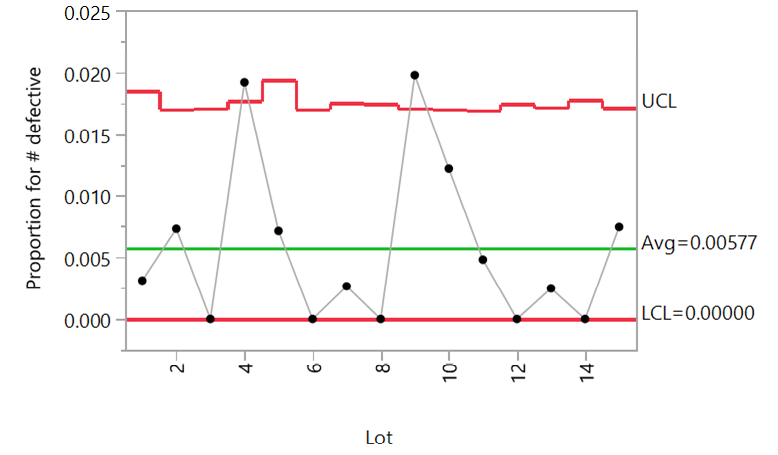
圖(1)
那麼,對於一些不符合特定分佈的資料,應該採用哪種管制圖呢?今天我們就介紹另外一種管制方式------分位數法。
什麼是分位數法?
回歸SPC的基本原理,我們需要一種可以甄別異常點的標準。SPC常規使用的管制圖都是通過設定一個管制限(Control Limit)來區分異常(Rule 1,其他暫且不談)。眾所周知,在標準分佈的情況下,管制限以外的區域的概率小於0.5%,小概率事件是我們需要研究的物件。借用相同的思路,在樣本量充足、但資料分佈不明確的情況下,我們通過分析資料的百分比分位數的方法來選擇一個固定值作為閾值(管制限),甄別小概率的產品批次,進而深入研究並評估風險。
那麼,如何使用分位數法來選擇管制限呢?這個就要取決於自身的風險設定了。比如我們在做假設檢驗時,很喜歡設定α= 0.05,β = 0.1 一樣。基於與傳統SPC一樣的管理標準,這裡暫定0.5% 意思就是基於歷史上的大資料,我們希望鑑別0.5%的批次進行進一步的評估和分析,如圖2所示。
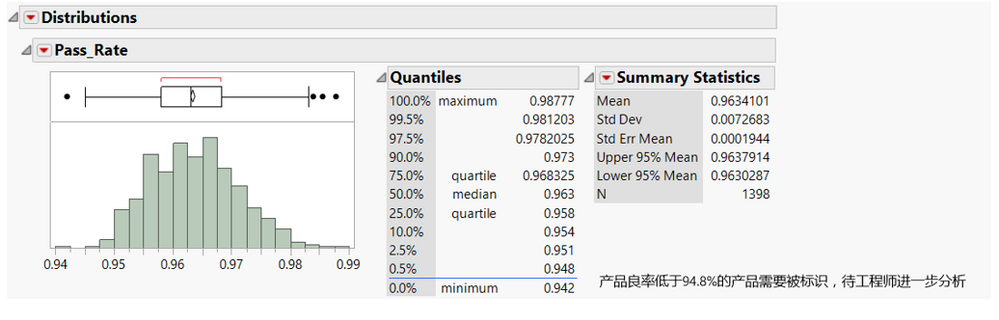 圖(2)
圖(2)
如何計算分位數?
分位數的計算其實很簡單,除了像圖2所示的長條圖外,JMP的“製表Tabulate”平臺可以批量性地計算每一種產品,每一種報廢類型,以及每一個層別的管制限,如圖3所示。根據自己資料庫的資料結構,你可以通過簡單拖曳的方式,這樣就可以快速得到想要的結果了。這裡有一點需要注意,產品良率和報廢率根據個人需要而選擇,因此分位元數的選擇是需要注意的。下圖中就是計算報廢率的分位數,因此計算時選用了99.5%的分位數作為管制限。
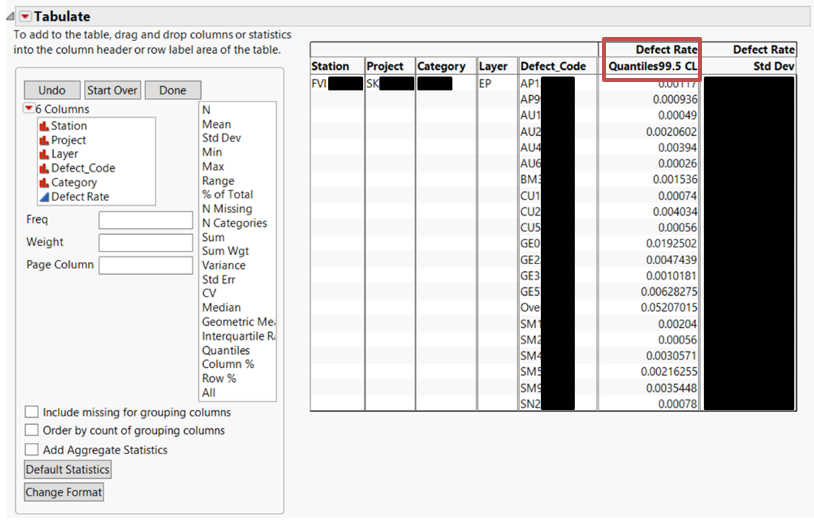
圖(3)
為什麼使用分位數法?
那麼,為什麼要使用分位數法呢?什麼時候適合使用?這種方法是否也會存在一定局限呢?
- 首先,分位元數法可以分析樣本結構不符合某種特定分佈的情況
當收集的樣本資料並不符合特定分佈時,強制計算管制限而得到的結果會存在偏差。在使用傳統的管制圖時,第一步都是對樣本資料進行分佈擬合,判斷資料是正態分佈、二項分佈或是卜瓦松分佈。如果分佈擬合差異很大,則需要轉化資料或增大樣本量後繼續分析,而分位元數法可以根據大資料的水準直接指定你需要的標準,從而彌補了傳統方法的缺陷。
- 計算管制限的方法簡單,途徑多樣
使用分位數法可以得到一個唯一的值作為管制標準,計算起來非常簡單而且有多種途徑進行計算。可以用專業的統計分析軟體實現,如JMP中的“分佈”(Distribution)、“製表”(Tabulate)功能,也可以使用Excel進行計算(將一組資料從大到小排列,通過資料總量計算出所需分位數的序號直接進行選擇)。
- 管制標準唯一,執行便利
由於採用分位數法計算,每個專案的管制限是唯一的。現場的QC可以根據管制表輕鬆地查詢出管制標準,進而確認是否需要暫停產品並通知工程師進行下一步的分析。(如果公司有生產管理系統,可以嘗試將管制表電子化,並與生產管理系統連結,實現自動化管制產品和通知的功能)。一段時間過後,當管制限更新時,可以由工程師下發新表,回收舊表進行管理(有自動管理系統的話可以刷新DB)。
而傳統的比例型管制圖,每個批次都需要計算管制規範,並記錄每個批次的結果是否符合規範。這樣的操作流程對於現場生產的QC要求很高。因此帶來人員管理上更高的要求,比如人員流動後所面臨的招聘和培訓工作,不利於現場管理和產品管制。
儘管分位數法上亮點眾多,但在使用時也存在一定的限制,比如:
- 對樣本量有要求
由於分位元數法是基於大資料的擬合方式,所以根據選取的標準對於樣本量是有要求的。例如10%的分位元數最少就需要10個批次才能達到最少解析度。0.5%分位元數就需要最少200個批次才區分。
- 不適合做新專案的管理
新產品、新專案的良率管制應該遵循設計良率的要求,根據標準製造能力和公差管理預測基本良率指標,隨後分析改善切入點,調整後提高產品批次品質,待項目正式放行後才開始收集資料並計算管制限。而分位元數法需要大樣本做基礎,不適合試產階段,並且試產階段時NPI(或類似部門)經常會調整設計或參數,因此結果會有較大的變化。觀測所有試產資料時會發現分層(如數據雙峰或多峰),不適合用任何一種管制圖管理。建議直接設定階段性目標管理,待新產品量產放行後,再做SPC的管理。
管制限是否需要更新?
通過以上說明,我們明白了分位數法管制SPC的思路。那麼,管制限設定後是否一成不變了呢?答案顯然是否定的。管制限應該基於實際的水準進行定期的更新。例如,生產線對於一個產品的生產經驗累積越來越多,產品良率自然會向好的方向發展,那麼管制限就應該選取一定週期的樣本重新計算。
當重新回顧並計算現有產品的管制限後,如何判斷是否需要更新管制限呢(因為樣本不同時,新的管制限或多或少會與原來的管制限有區別)?這裡因人而異,可以根據自身情況設定一個閾值。個人經驗是根據生產的長期波動水準制定閾值。如圖4,筆者就通過編輯公式得到閾值後自動判斷是否需要更新管制限。
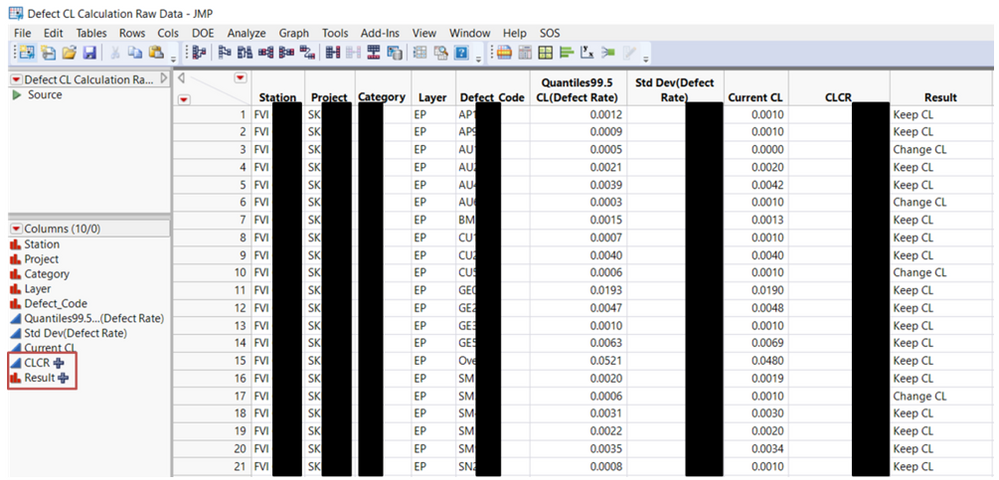
圖(4)列名後的+,代表本列有編輯公式。
JSL——自動化分析,事半功倍
由於產品眾多,且對應的報廢代碼更多,最後需要分析的工作量相當大,而且涉及到JMP的操作步驟也較多。為此,我們採用了JMP特有的JSL(JMP Script Language)程式碼,通過將具體的工作步驟進行錄製,然後保存並安裝,這樣下次使用的時候就可以一鍵分析啦,而無需每次從頭操作一遍,如下圖所示。
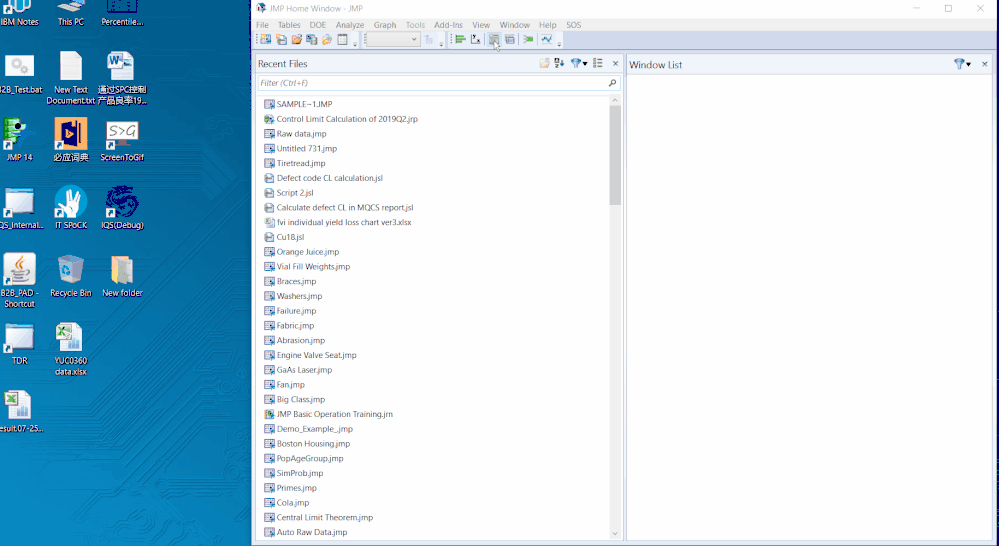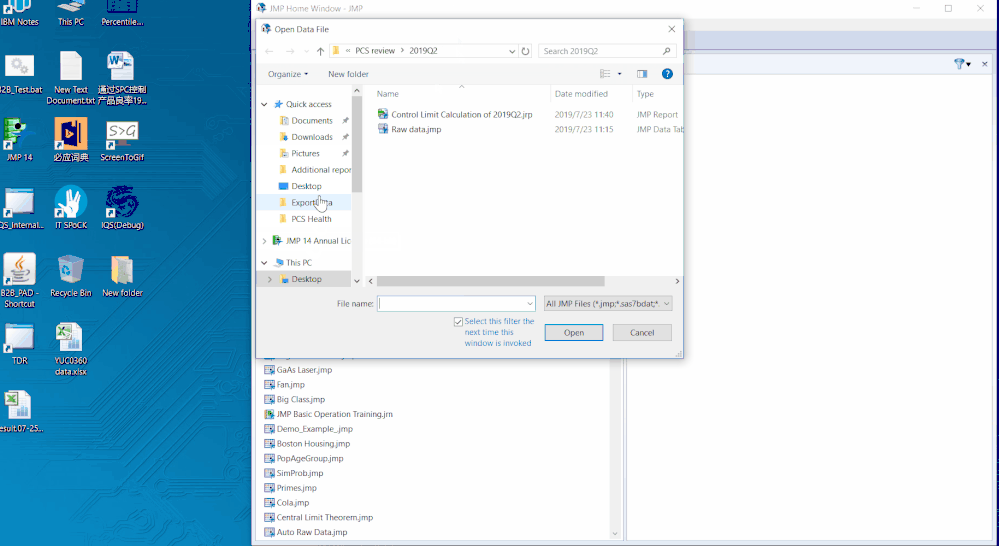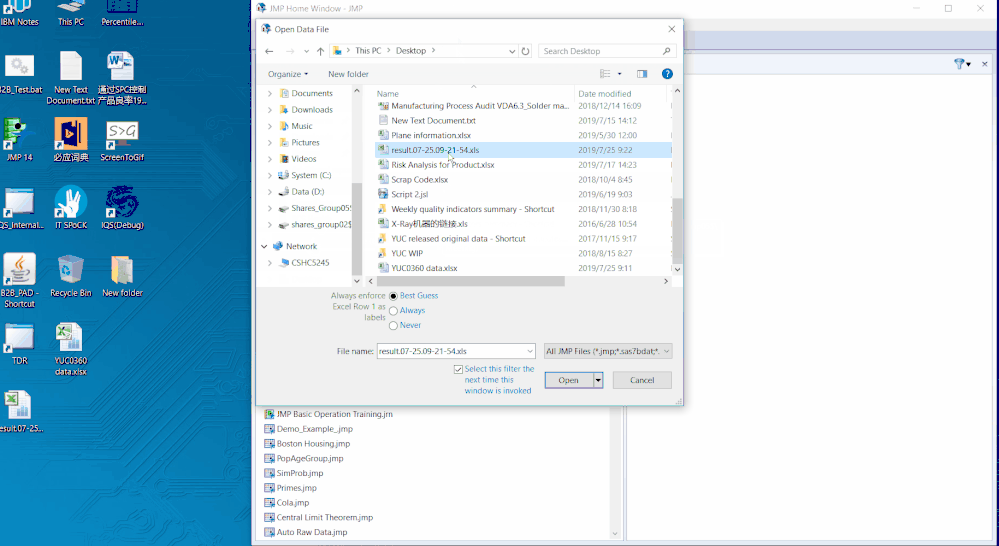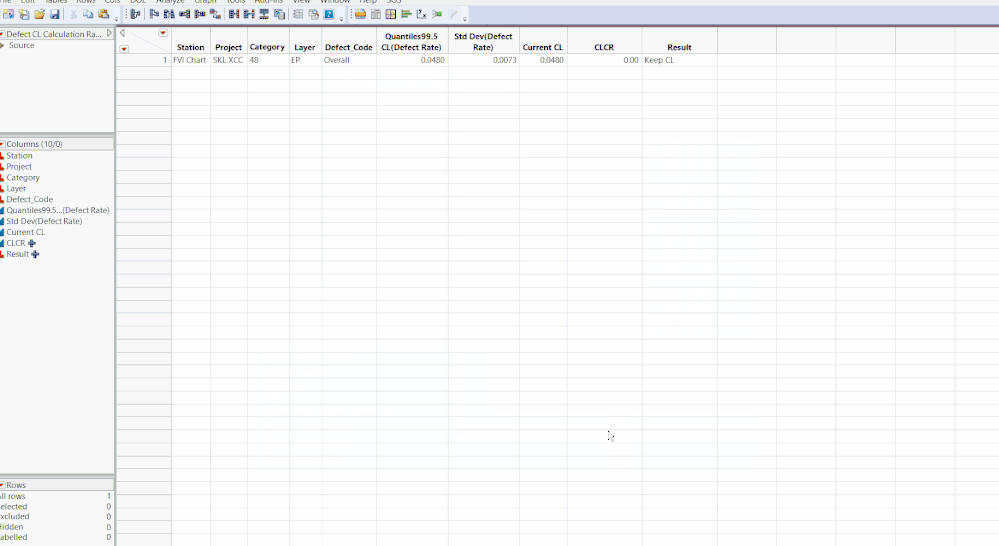
通過JSL,我們可以針對需要分析的資料進行批量型自動的分析,方便QE對所有產品的管制限定期回顧,這大大節省了QE的工作量和時間成本,從而把更多的精力投放在解決問題上而非鑑別問題。
You must be a registered user to add a comment. If you've already registered, sign in. Otherwise, register and sign in.